Meteorológiai esélylatolgatások
Latolgatáshoz kevés vagyok, a cikkek akiket Nektek is idéztem, azt a régóta (1977) ismert tényt részletezik, hogy a csapadék-képződés nem megy végbe masszív, és összetett, biológiai támogatás nélkül.
Most kezdünk közelíteni a fizikai valósághoz, t.i. hogy a tengerből párolgó kihullható csapadék a nyíltvíz, és partok felett ki is hullik. Hogy a felhők híján, nagy a napi hőingás, hogy az UV sugárzás erősebb Stratusok híján, és hogy felhők nélkül a földgolyó hő - cseréje leginkább szelek formájában valósul meg.
A konvektív csapadékkal is van egy kis gond, t.i. a celláknak ahhoz, hogy működjenek, térre / helyre van szükségük. Ha a légkörben olyan szennyezések vannak (metán, acetilén, stb), amelyek a felhőalapot följebb tolják, akkor a kihullható csapadék feláramlik az üllőbe, és nem igazán hull ki, mert sekély a légréteg, amiben a cellának dolgoznia kellene.
A masszív biológiai támogatást egy diverz élővilág hozta volt létre, elsősorban a tengerpartok élővilága, de amelyet a tengeri olajbányászat brutálisan tönkre is tett. A kisebb tech. malőrökről ne is beszéljünk, a gazdaság ezeket úgysem fogja valós értékükön kezelni, leírják a selejtbe a kiborult szennyet, azt' haladnak tovább... Kell az energija.
Mikor kölök voltam, egy autó volt az utcánkban, Vasáros Pista bá' rendőrautója, avval hordta a környék kiskölkeit a kórházba... de nem is volt mifelénk baja a szomszédaival senkinek. ma, ott tartunk, hogy már belépett egy újabb energiafaló, a szervertermek sokasága... filmeket és influenszereket nézünk rajta, a szomszéddal szóba se állunk már. Nem csak a fűtéssel van itt baj...
A régi bölcsek azt mondták, az Úristen a tenger mélyére veti az emberek bűneit...
Atyám fiai, a Tenger tele van.
Másképpen kellene csinálni, nagyon másképpen.
Most kezdünk közelíteni a fizikai valósághoz, t.i. hogy a tengerből párolgó kihullható csapadék a nyíltvíz, és partok felett ki is hullik. Hogy a felhők híján, nagy a napi hőingás, hogy az UV sugárzás erősebb Stratusok híján, és hogy felhők nélkül a földgolyó hő - cseréje leginkább szelek formájában valósul meg.
A konvektív csapadékkal is van egy kis gond, t.i. a celláknak ahhoz, hogy működjenek, térre / helyre van szükségük. Ha a légkörben olyan szennyezések vannak (metán, acetilén, stb), amelyek a felhőalapot följebb tolják, akkor a kihullható csapadék feláramlik az üllőbe, és nem igazán hull ki, mert sekély a légréteg, amiben a cellának dolgoznia kellene.
A masszív biológiai támogatást egy diverz élővilág hozta volt létre, elsősorban a tengerpartok élővilága, de amelyet a tengeri olajbányászat brutálisan tönkre is tett. A kisebb tech. malőrökről ne is beszéljünk, a gazdaság ezeket úgysem fogja valós értékükön kezelni, leírják a selejtbe a kiborult szennyet, azt' haladnak tovább... Kell az energija.
Mikor kölök voltam, egy autó volt az utcánkban, Vasáros Pista bá' rendőrautója, avval hordta a környék kiskölkeit a kórházba... de nem is volt mifelénk baja a szomszédaival senkinek. ma, ott tartunk, hogy már belépett egy újabb energiafaló, a szervertermek sokasága... filmeket és influenszereket nézünk rajta, a szomszéddal szóba se állunk már. Nem csak a fűtéssel van itt baj...
A régi bölcsek azt mondták, az Úristen a tenger mélyére veti az emberek bűneit...
Atyám fiai, a Tenger tele van.
Másképpen kellene csinálni, nagyon másképpen.
...és ez a "jó fejlett cikloncsalád" szépen borítja az eddig fennálló európai makroszinoptikus helyzetképet.  - mondjuk már ideje is. A portugálok kaptak elég esőt, de Algéria is. Míg a másik oldalon vastag mínuszokat mértek és terebélyes hóborítottság volt megfigyelhető.
- mondjuk már ideje is. A portugálok kaptak elég esőt, de Algéria is. Míg a másik oldalon vastag mínuszokat mértek és terebélyes hóborítottság volt megfigyelhető.
Köszönjük a kimerítő elemzést.
Laikusabb, amatőr megközelítésben én annyit szeretnék hozzátenni, hogy az Európa északi vidékei felett tapasztalt döntően magasnyomási uralom, ahogy összeomlik úgy erősödik meg az Azori szk.-i anticiklon hajlam függetlenül attól épp a modellek milyen vesszőfutásokat adnak. A magasnyomású hajlam ezúttal dél felől kezd majd "próbálkozni". Vannak erre jelek. Félblock szinte egészen valószínű, hogy várható, teljes blokkra még nem fogadnék.
Kérdés mind inkább az, hogy a Közép-Európába beszabaduló alacsony nyomású teknő áramlási rendszerével mennyire takarítja ki Európa északi részeiről a masszív hideget?
Lesz-e elég erős hideg hátoldalon Norvég-tenger felől? Netán meredekebb szögben Skandináv fsz. felől?
A bibi ott kezdődik, hogy az Északi-tenger felől érkező hideglégtömegeknek magasabb nedvességtartalma. Egyúttal magasabb harmatpontúak. Innentől kezdve sokkal vaskosabb hidegnek kell érkeznie már, hogy mind hó formában mint pedig nappali fagy tekintetében síkon igazán tél legyen. ((Persze ha Kárpát-medencében a hideglevegő nyugalomba jut (magasnyomás alatt), akkor kiszáradhat felettünk és viselkedhet ténylegesen száraz kontinentális hidegként, amire egy felcsúszó mediterrán ciklon okozhat kiterjedtebb síkvidéki havazást és nem kell aggódni a megmaradással sem.)) Mellesleg: (Minél több időt tölt szárazföld felett a hideglégtömeg annál alacsonyabb lesz a harmatpontja.)
Épp, ezért lyukadok ki oda mint 6 nappal ezelőtt körülbelül társalgóban is felvetettem, hogy 1-3 napos télies hidegöblités benne vannak most is a pakliban, de nagyobb hidegekre egyenlőre belátható időtávon belül reális esélyt nem látok. Akkor a febr.10-én többet tudunk majd-ot hoztam fel céldátumként, mivel nem volt tiszta a markováltás iránya. Most se épp az, de látszik, hogy félblock jó eséllyel lehet. S az által berántott, skandi ciklon hidegfrontjaként epizódszerűen beömlő hidegöblítések is, amit gyorsan követHET Azori orr / magasnyomás / ránk húzódása, majd félblockot lezáró Atlanti óceánon menetrend szerint közlekedő következő ciklon újra zonalitásra fordítja az áramlást.
Űridőbe látom kezdi dobálgatni a klasszikus blockingokat, tartósabb tél esélyeket, de bevallom őszintén nem tudok hinni neki. Lehet még télies idő, pálcát nem török felette, de inkább regionális szinten már. Dunántúl mákolhat mind novemberben tette vagy tartósabb északnyugati irányításnál hátoldalon lehetnek izgalmak. Lehet van bennem némi tavasz várás ennyi borongós, csergős idő után.
A csapadékhajlam továbbra is velünk marad, talán ennyi pozitívum van benne az előttünk álló időszakban.
Köszönjük a kimerítő elemzést.
Laikusabb, amatőr megközelítésben én annyit szeretnék hozzátenni, hogy az Európa északi vidékei felett tapasztalt döntően magasnyomási uralom, ahogy összeomlik úgy erősödik meg az Azori szk.-i anticiklon hajlam függetlenül attól épp a modellek milyen vesszőfutásokat adnak. A magasnyomású hajlam ezúttal dél felől kezd majd "próbálkozni". Vannak erre jelek. Félblock szinte egészen valószínű, hogy várható, teljes blokkra még nem fogadnék.
Kérdés mind inkább az, hogy a Közép-Európába beszabaduló alacsony nyomású teknő áramlási rendszerével mennyire takarítja ki Európa északi részeiről a masszív hideget?
Lesz-e elég erős hideg hátoldalon Norvég-tenger felől? Netán meredekebb szögben Skandináv fsz. felől?
A bibi ott kezdődik, hogy az Északi-tenger felől érkező hideglégtömegeknek magasabb nedvességtartalma. Egyúttal magasabb harmatpontúak. Innentől kezdve sokkal vaskosabb hidegnek kell érkeznie már, hogy mind hó formában mint pedig nappali fagy tekintetében síkon igazán tél legyen. ((Persze ha Kárpát-medencében a hideglevegő nyugalomba jut (magasnyomás alatt), akkor kiszáradhat felettünk és viselkedhet ténylegesen száraz kontinentális hidegként, amire egy felcsúszó mediterrán ciklon okozhat kiterjedtebb síkvidéki havazást és nem kell aggódni a megmaradással sem.)) Mellesleg: (Minél több időt tölt szárazföld felett a hideglégtömeg annál alacsonyabb lesz a harmatpontja.)
Épp, ezért lyukadok ki oda mint 6 nappal ezelőtt körülbelül társalgóban is felvetettem, hogy 1-3 napos télies hidegöblités benne vannak most is a pakliban, de nagyobb hidegekre egyenlőre belátható időtávon belül reális esélyt nem látok. Akkor a febr.10-én többet tudunk majd-ot hoztam fel céldátumként, mivel nem volt tiszta a markováltás iránya. Most se épp az, de látszik, hogy félblock jó eséllyel lehet. S az által berántott, skandi ciklon hidegfrontjaként epizódszerűen beömlő hidegöblítések is, amit gyorsan követHET Azori orr / magasnyomás / ránk húzódása, majd félblockot lezáró Atlanti óceánon menetrend szerint közlekedő következő ciklon újra zonalitásra fordítja az áramlást.
Űridőbe látom kezdi dobálgatni a klasszikus blockingokat, tartósabb tél esélyeket, de bevallom őszintén nem tudok hinni neki. Lehet még télies idő, pálcát nem török felette, de inkább regionális szinten már. Dunántúl mákolhat mind novemberben tette vagy tartósabb északnyugati irányításnál hátoldalon lehetnek izgalmak. Lehet van bennem némi tavasz várás ennyi borongós, csergős idő után.
A csapadékhajlam továbbra is velünk marad, talán ennyi pozitívum van benne az előttünk álló időszakban.
Köszönjük!!
Csak biztatni tudom a többieket is, hogy vegyék és vigyék tovább a fonalat. Kinek-kinek a maga szintjén, lehetőségein belül, mert minden meglátás érdekes lehet. Ezekre és hasonlóakra is (!) szükség van itt, csokorba gyűjtve és így szakmázva.
Mert én - bár magánügy -, de dögre unom magam a "de jó, hogy ez van, az van, tél fan vagyok, nyár fan vagyok" jellegű üres mondatoktól.
Mi a szögfrászt lehet abból elsajátítani...???
Tőlem legyen, csak legyen közben szakmai is, had lubickoljunk már kicsit
Nem szoktam nagyon nézni a reaíciókat egy-egy beírásra, de azért nektek orvosdoktoroknak e témában mégis jó visszajelzés a "véres kardot körbe vivő" kommentemben (nagyon képletesen értendő!!!) az a 32 poziítív visszacsatolás...nektek, nem nekem!...
És akadt köztük olyan akitől majd hanyat dőltem. hogy még itt van...Ősmentes és igen baráti viszonyt ápolt (gondolom most is ápol) egy nemes sportággal a vízilabdával... ...
...
És ha már állandóan lebulvározzuk akit amúgy valóban jogos és le kell bulvározni, akkor előtte a saját gerendákat meg közbe ki kellene kotorni....
Ezt a remek elemzést majd kissé koraibb, vagy későbbi, már nem tudom, időpontban próbálom megérteni
Csak biztatni tudom a többieket is, hogy vegyék és vigyék tovább a fonalat. Kinek-kinek a maga szintjén, lehetőségein belül, mert minden meglátás érdekes lehet. Ezekre és hasonlóakra is (!) szükség van itt, csokorba gyűjtve és így szakmázva.
Mert én - bár magánügy -, de dögre unom magam a "de jó, hogy ez van, az van, tél fan vagyok, nyár fan vagyok" jellegű üres mondatoktól.
Mi a szögfrászt lehet abból elsajátítani...???
Tőlem legyen, csak legyen közben szakmai is, had lubickoljunk már kicsit
Nem szoktam nagyon nézni a reaíciókat egy-egy beírásra, de azért nektek orvosdoktoroknak e témában mégis jó visszajelzés a "véres kardot körbe vivő" kommentemben (nagyon képletesen értendő!!!) az a 32 poziítív visszacsatolás...nektek, nem nekem!...
És akadt köztük olyan akitől majd hanyat dőltem. hogy még itt van...Ősmentes és igen baráti viszonyt ápolt (gondolom most is ápol) egy nemes sportággal a vízilabdával...
És ha már állandóan lebulvározzuk akit amúgy valóban jogos és le kell bulvározni, akkor előtte a saját gerendákat meg közbe ki kellene kotorni....
Ezt a remek elemzést majd kissé koraibb, vagy későbbi, már nem tudom, időpontban próbálom megérteni
Örülök, ha van aki olvassa, értékeli, és érti, már ha érthetően írom, amit írok , de az alapvetően inkább szemléletformálás akarna lenni, már akinek van erre vevő antennája...ezért kerül a sajnos, vagy nem sajnos a látogatottabb Met. társalgóba...hátha csak egy picit is előrébb mozdulunk...mert egyszer ennek a tankernek, amin mindannyian ülünk, a kormánykerekét el kell forgatni 180 fokkal, mert nagyon jön a jéghegy és még akkor is 10 km-en át egyenesen fog menni a tehetetlensége miatt, míg nem kanyarodni nem kezdünk...a nagyon képszerű, de érthető hasonlat nem az enyém, lopom dr Borovics Attilától, az Erdészeti Tudományos Intézet főigazgatójától...
, de az alapvetően inkább szemléletformálás akarna lenni, már akinek van erre vevő antennája...ezért kerül a sajnos, vagy nem sajnos a látogatottabb Met. társalgóba...hátha csak egy picit is előrébb mozdulunk...mert egyszer ennek a tankernek, amin mindannyian ülünk, a kormánykerekét el kell forgatni 180 fokkal, mert nagyon jön a jéghegy és még akkor is 10 km-en át egyenesen fog menni a tehetetlensége miatt, míg nem kanyarodni nem kezdünk...a nagyon képszerű, de érthető hasonlat nem az enyém, lopom dr Borovics Attilától, az Erdészeti Tudományos Intézet főigazgatójától...
Kissé zavarba is hoz a köszönettel vett kedves biztatás, mert ebbe a fórumba nem tudom, hogy illeszkedne bele mindez... (döntsék el a modik, ha kísérlet tehető rá, akkor lehet ezzel az szakmai hosszú- és középtávú esélylatolgatások farvizén, néha csendben a partvonalon foglalkozni itt is, főleg, ha több erdőökológiai szakmaiságot veszek alapul...)
Ettől függetlenül, az erdő mint a legbonyolultabb és legösszetettebb szárazföldi ökoszisztéma rendszer, amiről kb. szerintem semmit, vagy csak alig valamit tudunk úgy valójában (csak az óceánok világa bonyolultabb ennél) sokkalta sokrétűbb és bonyolultabb, mint maga a légkör, annak akár globális léptékében is....egy erdő oda-vissza csatolási folyamatainak a száma kvázi végtelenek...a mikrovilág mely egy erdőben mindent meghatároz, már a gombák szintjén is olyan bonyolult, hogy evolúció biológus legyen a talpán aki megérti egy töredékét is...vagy ha csak a szénkörforgás részét képező citromsav ciklusra gondolok, már az is elképesztő...életemben egyszer láttam leírva a Krebs-ciklus és az azt kiegészítő, egymásba kapcsolódó fotoszintézis teljes egyenletét leírva...hát, jó, hogy elég volt a két bazi nagy egyetemi tábla a felére, és még jobb, hogy csak demonstárció szinten kellett látni ..
..
Ez az általános csak a felszínt kapargatja
Link
Az erdő és annak élőlényei előrejelezni nyilván nem tudnak, vagy csak nagyon rövid távon érzik meg pl. egy erősebb hidegbetörés, vagy porhavazás "szagát, jeleit"...egy madáretetőn ez jól tanulmányozható télen...érzik, amit a homo sapiens (bölcs???) már nem, mert kilépett a természetes ciklusokból...
Egy kékcinege nem engedheti meg magának, hogy legalább egy nappal előre ne érezzen rá a változásra és ne kezdjen el plusz élelem források után nézni, mert a 41-42 fokos testhőmérsékletet mínusz 20 fokos éjjelen, pl. 10 órán át megőrizni az nagyon kemény menet és tiszteletreméltó teljesítmény egy grammokban mérhető kis madár esetében ...ki lehet próbálni a mi kis 36,5 fokunkkal és túlsúlyunkkal, milyen lenne ez odakinn....
Az erdőt egésznek véve, mégis van benne egy fajta rendszerszintű leképződése a várható közeljövőnek...(nem muflonzsír vastagság szinten, az max parányi része lehet)
Csak a mai tudománynak az a baja, hogy szétszedi atomjaira ezeket a rendszereket, analizálja a béka seggéig, majd megpróbálja összerakni és a végén kiderül, hogy ez nem megy, nem áll össze és nem érti, hogy mi a baj ...áll a mikrobiológus a 16 szerzős, agyon citált indexű cikkel a kezében és az egész, ahogy van nem illeszkedik bele a nagy rendszerbe hiába préseli...de mindegy is, mert ha megugorja a tudománymetriai szinteket, akkor publikálható és kész, ennyi a lényeg....
Egy evolúció biológus, 20 évig dolgozik 1 db (!!) cikkel...hát ezt a műfajt ma kevésbé díjazzák....
És a nagy analízis után mindez azért, nem áll össze, mert a rendszer önmagában hordozott egészlegességének saját alaptörvényszerűségeit, nem lehet kiemelni az egészből...önmagában hordozza...én kevés vagyok, hogy ezt érthetően elmagyarázzam, ehhez legalább egy Mátyás Csaba, Vida Gábir kellene...a könyveiket érdemes elolvasni...
Egyébként ezért kellene a meteorológusoknak, klimatológusoknak is biológiát és ökológiát tanulnia és vica versa!!!
Főleg, globális légkörzés szinten, mert pl. egy ökológus a mikroklímában, mezoklímában otthon van, de hogy mi az hogy hipertrópusi éghajlat, hát arról nem sok fogalma van és sorolhatnánk
(Én kicsit (!!!) könnyebben ugrálok úgy mond, mert van egy földraj szakos alapom, ahol az ÁC megkerülhetetlen stúdium - szóró tantárgy - persze nem meteorológus szinten...de kapásból mondok tíz Metnetest, aki lelkes amatőrként is profi ebben...max. csak már vagy nincs rég itt, vagy nem ír, csak időnként olvas...
Egy példa az erdőhöz: a nagyon egzakt FAI-index (erdészeti aszályindex) kimunkálása, és az ehhez rendelhető döntéstámogatói modellek (pl. Site Viewer) erdészeti kezeléseket meghatározó klímaforgatókönyv verziók modelleljeiben ezt egészlegességet figyelembe is veszik.... akár globális légkörzés léptékében is...gondoljunk csak a jó nagy mértékben elhallgatott jégmagképző baktériumok fontosságára, és az óceáni kén biogeokémiai ciklusra, összefüggésben a plankton élővilággal....az óceánok feletti csapadékképzőséssel és ezek kontinentális hatásaival....Márti (gulyásme) köteteket tudna beszélni erről...
Kissé zavarba is hoz a köszönettel vett kedves biztatás, mert ebbe a fórumba nem tudom, hogy illeszkedne bele mindez... (döntsék el a modik, ha kísérlet tehető rá, akkor lehet ezzel az szakmai hosszú- és középtávú esélylatolgatások farvizén, néha csendben a partvonalon foglalkozni itt is, főleg, ha több erdőökológiai szakmaiságot veszek alapul...)
Ettől függetlenül, az erdő mint a legbonyolultabb és legösszetettebb szárazföldi ökoszisztéma rendszer, amiről kb. szerintem semmit, vagy csak alig valamit tudunk úgy valójában (csak az óceánok világa bonyolultabb ennél) sokkalta sokrétűbb és bonyolultabb, mint maga a légkör, annak akár globális léptékében is....egy erdő oda-vissza csatolási folyamatainak a száma kvázi végtelenek...a mikrovilág mely egy erdőben mindent meghatároz, már a gombák szintjén is olyan bonyolult, hogy evolúció biológus legyen a talpán aki megérti egy töredékét is...vagy ha csak a szénkörforgás részét képező citromsav ciklusra gondolok, már az is elképesztő...életemben egyszer láttam leírva a Krebs-ciklus és az azt kiegészítő, egymásba kapcsolódó fotoszintézis teljes egyenletét leírva...hát, jó, hogy elég volt a két bazi nagy egyetemi tábla a felére, és még jobb, hogy csak demonstárció szinten kellett látni
Ez az általános csak a felszínt kapargatja
Link
Az erdő és annak élőlényei előrejelezni nyilván nem tudnak, vagy csak nagyon rövid távon érzik meg pl. egy erősebb hidegbetörés, vagy porhavazás "szagát, jeleit"...egy madáretetőn ez jól tanulmányozható télen...érzik, amit a homo sapiens (bölcs???) már nem, mert kilépett a természetes ciklusokból...
Egy kékcinege nem engedheti meg magának, hogy legalább egy nappal előre ne érezzen rá a változásra és ne kezdjen el plusz élelem források után nézni, mert a 41-42 fokos testhőmérsékletet mínusz 20 fokos éjjelen, pl. 10 órán át megőrizni az nagyon kemény menet és tiszteletreméltó teljesítmény egy grammokban mérhető kis madár esetében ...ki lehet próbálni a mi kis 36,5 fokunkkal és túlsúlyunkkal, milyen lenne ez odakinn....
Az erdőt egésznek véve, mégis van benne egy fajta rendszerszintű leképződése a várható közeljövőnek...(nem muflonzsír vastagság szinten, az max parányi része lehet)
Csak a mai tudománynak az a baja, hogy szétszedi atomjaira ezeket a rendszereket, analizálja a béka seggéig, majd megpróbálja összerakni és a végén kiderül, hogy ez nem megy, nem áll össze és nem érti, hogy mi a baj ...áll a mikrobiológus a 16 szerzős, agyon citált indexű cikkel a kezében és az egész, ahogy van nem illeszkedik bele a nagy rendszerbe hiába préseli...de mindegy is, mert ha megugorja a tudománymetriai szinteket, akkor publikálható és kész, ennyi a lényeg....
Egy evolúció biológus, 20 évig dolgozik 1 db (!!) cikkel...hát ezt a műfajt ma kevésbé díjazzák....
És a nagy analízis után mindez azért, nem áll össze, mert a rendszer önmagában hordozott egészlegességének saját alaptörvényszerűségeit, nem lehet kiemelni az egészből...önmagában hordozza...én kevés vagyok, hogy ezt érthetően elmagyarázzam, ehhez legalább egy Mátyás Csaba, Vida Gábir kellene...a könyveiket érdemes elolvasni...
Egyébként ezért kellene a meteorológusoknak, klimatológusoknak is biológiát és ökológiát tanulnia és vica versa!!!
Főleg, globális légkörzés szinten, mert pl. egy ökológus a mikroklímában, mezoklímában otthon van, de hogy mi az hogy hipertrópusi éghajlat, hát arról nem sok fogalma van és sorolhatnánk
(Én kicsit (!!!) könnyebben ugrálok úgy mond, mert van egy földraj szakos alapom, ahol az ÁC megkerülhetetlen stúdium - szóró tantárgy - persze nem meteorológus szinten...de kapásból mondok tíz Metnetest, aki lelkes amatőrként is profi ebben...max. csak már vagy nincs rég itt, vagy nem ír, csak időnként olvas...
Egy példa az erdőhöz: a nagyon egzakt FAI-index (erdészeti aszályindex) kimunkálása, és az ehhez rendelhető döntéstámogatói modellek (pl. Site Viewer) erdészeti kezeléseket meghatározó klímaforgatókönyv verziók modelleljeiben ezt egészlegességet figyelembe is veszik.... akár globális légkörzés léptékében is...gondoljunk csak a jó nagy mértékben elhallgatott jégmagképző baktériumok fontosságára, és az óceáni kén biogeokémiai ciklusra, összefüggésben a plankton élővilággal....az óceánok feletti csapadékképzőséssel és ezek kontinentális hatásaival....Márti (gulyásme) köteteket tudna beszélni erről...
Sziasztok! Egy latolgatás az utolsó dekád elejére, illetve kiindulásként az elmaradt PV összeomlásról: 
A következő pár napban kihagyott ziccer (teljes blokk kialakulása és SSW): a télies fordulat ellen hat, akár hosszabb távon is. Kár, hogy a grönlandi és a sarki AC egyesülése nem bír(t) még délebbre hatolni. Ezzel a novemberi épp, hogy csak SSW-hez hasonló helyzet állt volna fel. Február elejére változtak meg az előrék: gyengítették az AC grönlandi és attól délre lévő részét, az ECM zónaszél előre is ekkor fordult vissza a 0 irányából, ahogy visszanézhető az ECM honlapján.
ECM fáklya átlag jan. végi vs.. febr. 2-i előréből:
Link
Link
Illetve a GFS örvényt gyengítő fluxusokat mutató metszete is erről tanúskodik, a nyugati féltekén az alsó sztratoszféráig felnyúló barnás árnyalatú örvénygyengítő hőáramlásai a negatív fluxusok, vagyis a kékes árnyalat felé tolódtak. Látszik, hogy a vertikális térszerkezetben (fehér kontúrok) is a grönlandi AC előrejelzett mezeje változott nagyon, de az Amerika feletti helyzet is negatívan változott.
Link
Link
Itt egyébként nem is egy még erősebb örvénygyengülés lett volna a lényeg, hanem maga a blokk, hiszen helyette egy jól fejlett cikloncsalád érkezik meg majd az óceánról. Link
Majd az óceáni újabb ciklon előoldalán ÉK-i irányba felnyomuló azori-AC nyúlvány nem engedi, hogy jobb rétegződésű hideg levegő érkezzen meg, illetve a képződő (második) medi túl délre mehet el (klasszikus, ha fel is ér a csapi, az is az érdemi hideg érkezése előtt).
Mi várható ezt követően?
Most tehát a blokk túl északon maradása volt a gond. 20-a után viszont egy újabb AC jelenhet meg az óceánon, ezúttal azonban az azori AC irányából, és abban a helyzetben pedig a blokk északra kiterjedése lehet a probléma, továbbá túl nyugati kialakulás is körvonalazható, valamint azért a hosszabbodó nappalok is jelenthetnek problémát, ha mégis jobb felállás jelenne meg. Az északra való felhatolás, és egy teljes, szinkronban lévő blokk felállása ellen szólhat a vertikális (örvény)szerkezet rossz irányú változása: miközben jelenleg az atlanti térségben északon van a grönlandi AC a troposzférában, és ez felnyúlik nagy magasságba (az örvényt megnyúlásra kényszerítő magassági AC képében), délebbre pedig az óceáni csigákat látjuk az alsó légkörben:
Link
Link
Addig az űrtávú várakozásban a délebbi térségben az AC jelen van ( és itt van egy olyan változás is, hogy a körformához közelebb álló, nem megnyúlt örvény melletti anticiklonális ellenörvényhez kapcsolódik), viszont az északabbi metszeten jól látszik, hogy egy keletibb, jobb pozíciójú talajon lévő AC-t kevésbé enged meg a sztratoszférikus örvény
Link
Link
Ezt alátámaszthatja az előrejelzett, pozitívba váltó AO index is, bár a végén ismét van lefelé szórás is:
Link
Ez visszaköszön az ECM ENS friss klaszter előrejelzésében is, valamilyen gerincesedés megindul, de egyik sem a legjobb helyzetben ezen fő forgatókönyvek szerint:
Link
Egy pozitív dolog van a friss 12-es ECM ENS-ben, az pedig az 50-es taggal jellemezhető eslő forgatókönyv, hogy a ciklonális mező masszívabb lesz, és 15-16 után is benne van a pakliban legalább nagyobb csapadék érkezése, fáklyán látható is erre jel, feltételezésem szerint ez mind az első klaszter tagjaiból származik:
Link
Link
A következő pár napban kihagyott ziccer (teljes blokk kialakulása és SSW): a télies fordulat ellen hat, akár hosszabb távon is. Kár, hogy a grönlandi és a sarki AC egyesülése nem bír(t) még délebbre hatolni. Ezzel a novemberi épp, hogy csak SSW-hez hasonló helyzet állt volna fel. Február elejére változtak meg az előrék: gyengítették az AC grönlandi és attól délre lévő részét, az ECM zónaszél előre is ekkor fordult vissza a 0 irányából, ahogy visszanézhető az ECM honlapján.
ECM fáklya átlag jan. végi vs.. febr. 2-i előréből:
Link
Link
Illetve a GFS örvényt gyengítő fluxusokat mutató metszete is erről tanúskodik, a nyugati féltekén az alsó sztratoszféráig felnyúló barnás árnyalatú örvénygyengítő hőáramlásai a negatív fluxusok, vagyis a kékes árnyalat felé tolódtak. Látszik, hogy a vertikális térszerkezetben (fehér kontúrok) is a grönlandi AC előrejelzett mezeje változott nagyon, de az Amerika feletti helyzet is negatívan változott.
Link
Link
Itt egyébként nem is egy még erősebb örvénygyengülés lett volna a lényeg, hanem maga a blokk, hiszen helyette egy jól fejlett cikloncsalád érkezik meg majd az óceánról. Link
Majd az óceáni újabb ciklon előoldalán ÉK-i irányba felnyomuló azori-AC nyúlvány nem engedi, hogy jobb rétegződésű hideg levegő érkezzen meg, illetve a képződő (második) medi túl délre mehet el (klasszikus, ha fel is ér a csapi, az is az érdemi hideg érkezése előtt).
Mi várható ezt követően?
Most tehát a blokk túl északon maradása volt a gond. 20-a után viszont egy újabb AC jelenhet meg az óceánon, ezúttal azonban az azori AC irányából, és abban a helyzetben pedig a blokk északra kiterjedése lehet a probléma, továbbá túl nyugati kialakulás is körvonalazható, valamint azért a hosszabbodó nappalok is jelenthetnek problémát, ha mégis jobb felállás jelenne meg. Az északra való felhatolás, és egy teljes, szinkronban lévő blokk felállása ellen szólhat a vertikális (örvény)szerkezet rossz irányú változása: miközben jelenleg az atlanti térségben északon van a grönlandi AC a troposzférában, és ez felnyúlik nagy magasságba (az örvényt megnyúlásra kényszerítő magassági AC képében), délebbre pedig az óceáni csigákat látjuk az alsó légkörben:
Link
Link
Addig az űrtávú várakozásban a délebbi térségben az AC jelen van ( és itt van egy olyan változás is, hogy a körformához közelebb álló, nem megnyúlt örvény melletti anticiklonális ellenörvényhez kapcsolódik), viszont az északabbi metszeten jól látszik, hogy egy keletibb, jobb pozíciójú talajon lévő AC-t kevésbé enged meg a sztratoszférikus örvény
Link
Link
Ezt alátámaszthatja az előrejelzett, pozitívba váltó AO index is, bár a végén ismét van lefelé szórás is:
Link
Ez visszaköszön az ECM ENS friss klaszter előrejelzésében is, valamilyen gerincesedés megindul, de egyik sem a legjobb helyzetben ezen fő forgatókönyvek szerint:
Link
Egy pozitív dolog van a friss 12-es ECM ENS-ben, az pedig az 50-es taggal jellemezhető eslő forgatókönyv, hogy a ciklonális mező masszívabb lesz, és 15-16 után is benne van a pakliban legalább nagyobb csapadék érkezése, fáklyán látható is erre jel, feltételezésem szerint ez mind az első klaszter tagjaiból származik:
Link
Link
Magam pedig a Te megfigyeléseidre és az ezen alapuló fejtegetések írására biztatnálak. Nem vagyok erdész-szakmabeli, mindössze "lelkes műkedvelő", de nagyon tanulságosak a bejegyzéseid.
Nyuli, Rudolfking, KP, Viharkém, csokitó18 és a többi magister "orvosdoktorok", ebben és más a fórumhoz kapcsolódó témában, csak kérni tudom, szerintem többek nevében, hogy ezt a végre a Metnet igazi arcára hasonlító szakmai diskurzust, amiből csak tanulni tudunk, mi csökkent értelmű medvebocsok e téren , ne hagyjátok abba, ha időtök, kedvetek engedi, és ha már végre megmozdult ez a szerintem nagyon fontos fórum élete.! Mondhatnám: a témák az asztalon hevernek, gondoskodik erről az időjárás. Én élvezettel olvasom...
, ne hagyjátok abba, ha időtök, kedvetek engedi, és ha már végre megmozdult ez a szerintem nagyon fontos fórum élete.! Mondhatnám: a témák az asztalon hevernek, gondoskodik erről az időjárás. Én élvezettel olvasom...
Egy csomó érdekesség van ezekben a forrásokban (messze pöpecebb, mint az LLM), eddig pl. sose hallottam a "stratospheric wave reflection index"-ről, és az se volt eddig nyilvánvaló nekem, hogy egy jó major SSW, split stb. sem mindig fentről indul. Nem mindig kellenek azok a keleties szelek sem (én linkjeimen 0 alatti értékek) ahhoz, hogy polar vortex disruption-ről (sarki örvény zavaráról) és hidegbetörésekről beszélhessünk, ennél sokkal komplexebb a kép.
Na persze most a hosszútávú előréket nézve ráfaragtunk, és az USA-ban is visszavonul a hideg ( Link ) szóval tippre visszaáll az örvény alacsonyabb szinteken, és a magasabb szinten készülődő zavarások könnyen lehet, hogy csak február második felét befolyásolják. Február elejére viszont tényleg vannak erős futások a poláris örvény melegedését illetően.
Na persze most a hosszútávú előréket nézve ráfaragtunk, és az USA-ban is visszavonul a hideg ( Link ) szóval tippre visszaáll az örvény alacsonyabb szinteken, és a magasabb szinten készülődő zavarások könnyen lehet, hogy csak február második felét befolyásolják. Február elejére viszont tényleg vannak erős futások a poláris örvény melegedését illetően.
Köszi, szerintem teljesen jól rávilágítottál a kritikus pontokra. A vitatott részekkel kapcsolatban az az én meglátásom, hogy az LLM-eket az viszi nagyon félre a "már bekövetkezett" és a "várhatóan meg fog történni" értelmezése során, hogy a felhasznált elemzésekben hivatkozott előrejelzési térképek dátumait nem nézik a webes böngészés során, csak a szöveget.
A másik - emberi - oldala, hogy az elérhető elemzések, vagy blogbejegyzések kicsit hajlamosak a szenzációhajhászásra, mert a sok hír között esély sem lenne érvényesülniük, ami kicsit tovább torzítja a képet.
A szakmai részt illetvően itt vannak a felhasznált elemzések, amelyekből végül szintézis készült:
Link
Link
Link
Link
Link
A másik - emberi - oldala, hogy az elérhető elemzések, vagy blogbejegyzések kicsit hajlamosak a szenzációhajhászásra, mert a sok hír között esély sem lenne érvényesülniük, ami kicsit tovább torzítja a képet.
A szakmai részt illetvően itt vannak a felhasznált elemzések, amelyekből végül szintézis készült:
Link
Link
Link
Link
Link
Vakarom a fejem ezen az AI összefoglalón.... Tényleg volt SSW január közepén? Link Itt az időben is oda-vissza lehet menni, ez még minor SSW-nek is gyenge, ha egyáltalán hívhatjuk annak. Az AI által említett major pedig sehol sincs, nem fordultak a szelek keletire, ld. korábbi linkem. Honnan hallucinálta ezt? (mért szelek: Link innen: Link A 2025 november végi pedig eléggé mellément, elnézve legalábbis az előrejelzéseket: ugye akkor már a hideg és a havazás idején voltunk és utána hosszú nyugati áramlásos időszak következett elég sok enyhe időszakkal (itt-ott melegrekordok stb.). A vége se lett a hónapnak túl hideg (az említett Németországban legalábbis), se tavak nem fagytak rendesen be, se hó nem esett sok, semmi keleti beast, és ha nincs köd állandóan, még München se mért volna állandóan 0 körüli T-ket. A száraz január se jött be nálatok legalábbis, itt kevés a csapadék, és ez így is marad, de szép csapadékkal indított az év első hónapja. De persze 2 hónapra előre, chatGPT, nem akarok ítélkezni, bölcsebb, mint sok előrejelzés, amibe bele kell futnunk. Csak beképzelt dolgokat.
Ennek fényében honnan szedte 2 napja, hogy SSW volt? Ráadásul major (tehát 10 hPa-n megfordultak a szelek)? Ez pedzegette decemberben, de major SSW-t nem mert nyilván állítani: Link sőt, azt állítja, hogy a december eleji nagy (épp hogy major?) SSW óta a poláris örvény beröffent, sőt erősebb, mint az átlag (ez azóta nem teljesen így lett, gyengébb, de sehol egy SSW). Kiemelte a blogposzt, hogy az alsó poláris örvény most épp, hogy engedte a hideg lábakat többek között Közép-Európára is, pedig felette az örvény nem volt megzavarodva / legyengülve.
Azt is hallucinálgatja, hogy akkor most jön január végére még egy SSW, de ennek is ellentmondanak az előrejelzések, ma is, meg tegnapelőtt is. Link ez a 17-ei előrejelzés, itt az örvényen még nyoma sincs. Még a bemelegedés is csak a hó végére várható (szokásos bizonytalanság mellett)...
Őszinte leszek, nekem Nyuli "színvonaltalan" elemzése profibbnak, precízebbnek és pontosabbnak tűnik, igaz, sokkal kevesebb mágikus szakszóval és még kevesebb hideg téli "száraz, de hóviharos" ígérettel.
Ennek fényében honnan szedte 2 napja, hogy SSW volt? Ráadásul major (tehát 10 hPa-n megfordultak a szelek)? Ez pedzegette decemberben, de major SSW-t nem mert nyilván állítani: Link sőt, azt állítja, hogy a december eleji nagy (épp hogy major?) SSW óta a poláris örvény beröffent, sőt erősebb, mint az átlag (ez azóta nem teljesen így lett, gyengébb, de sehol egy SSW). Kiemelte a blogposzt, hogy az alsó poláris örvény most épp, hogy engedte a hideg lábakat többek között Közép-Európára is, pedig felette az örvény nem volt megzavarodva / legyengülve.
Azt is hallucinálgatja, hogy akkor most jön január végére még egy SSW, de ennek is ellentmondanak az előrejelzések, ma is, meg tegnapelőtt is. Link ez a 17-ei előrejelzés, itt az örvényen még nyoma sincs. Még a bemelegedés is csak a hó végére várható (szokásos bizonytalanság mellett)...
Őszinte leszek, nekem Nyuli "színvonaltalan" elemzése profibbnak, precízebbnek és pontosabbnak tűnik, igaz, sokkal kevesebb mágikus szakszóval és még kevesebb hideg téli "száraz, de hóviharos" ígérettel.
KP, köszönjük, égetően nagy szükség van itt a Metneten ilyen színvonalú szakmai elemzésekre és prognózisokra (is!), a beválásuk verifikálásával együtt.
Régen nem esett szó az SSW-kről, ezért kommentár nékül küldök két LLM által készített összefoglalót. Az első még Katalin napon (2025.nov.25) készült, a másik meg egy aktuális mostani frissítés. Íme:
Legfrissebb fejlemények (2025. november 25.)
Jelenleg egy rekord korai SSW esemény zajlik november végén, amely az egyik legkorábbi a megfigyelések történetében (csak a harmadik ilyen az elmúlt 70 évben novemberben). A poláris örvény deformálódása már megkezdődött, a csúcs november 25. körül várható, és a hatások 2–3 héten belül, december elején jelentkezhetnek. Ez a jelenség elsősorban Észak-Amerikát érinti kezdetben, de Európára is hatással lesz, különösen késő decemberben. A La Niña jelenség tovább erősítheti a hideg trendeket, de a stratoszferikus változások dominálnak.
Hatások Európára és Közép-Európára a 2025/2026-os télre
Az előrejelzések vegyesek, de összességében hidegebb és változékonyabb telet várnak, mint amit korábban prognosztizáltak. A svájci MeteoSwiss óvatosságra int: bár a poláris örvény gyengül, a hatások nem feltétlenül terjednek le a felszínre, és az európai tél enyhébb maradhat, mint az "évszázad telel" spekulációk sugallják. Decemberben kicsi a hideg tél valószínűsége, januártól pedig az átlag feletti hőmérséklet várható .
Hőmérséklet-előrejelzések december:
Normál vagy hidegebb az átlagnál Nyugat- és Közép-Európában (pl. Svájc, Németország, Lengyelország), keleties hideg áramlás miatt. Késő decemberben "Kelet fenevadja" (Beast from the East) típusú hideg hullám lehetséges, ami -10 °C alatti értékeket hozhat Közép-Európába. Január: Semleges vagy kissé hidegebb Közép-Európában, szárazabb, hűvösebb levegővel a magasnyomás miatt.Február: Általában melegebb az átlagnál az egész kontinensen, de hidegebb kezdet vagy vég lehetséges.
Csapadék és havazás
december: Növekvő hótakaró Nyugat- és Közép-Európában, jelentős havazás várható a hideg levegő beáramlásával.Január: Alacsonyabb csapadékmennyiség, szárazabb körülmények.Február: Átlagos csapadék Közép- és Nyugat-Európában, több eső/hó az északi részeken.
Regionális fókusz – Közép-Európa (pl. Svájc, Ausztria, Magyarország, Lengyelország):Hidegebb anomáliák decemberben, keleties áramlás miatti hideg beáramlás. A poláris örvény összeomlása főként Észak-Amerikát érinti kezdetben, de Európában enyhébb nyugati áramlás után december végére erősödik a hideg. Történelmi példák (pl. 1958, 1968-as SSW-k) hasonló korai eseményeknél gyengébb hűtést mutattak Észak-Közép-Európában, de a mostani eset erősebb lehet.
Friss X (korábbi Twitter) posztok és vélemények Az X-en is élénk a vita:
A Ventusky figyelmeztet a korai SSW-re, ami hideg arkticus levegőt hozhat Európába, Észak-Amerikába és Ázsiába.Mark Vogan meteorológus élő adásban tárgyalta a hideg, havas Nyugat-Európát.Francia források (CATastrophesNATurelles) megerősítik a hidegebb telet Európában december végéig.
SSW Státusz Frissítés (2026. január 17.)
A legfrissebb adatok alapján (pl. ECMWF, GFS modellek és meteorológiai elemzések) egy aktív Sudden Stratospheric Warming (SSW) esemény zajlik 2026 januárjában. Ez egy major (jelentős) SSW, amely a poláris örvény (polar vortex) erős zavarát okozza, és már január közepén tetőzött. A stratoszférában a hőmérséklet-anomáliák +25–50 °C-os emelkedést mutatnak az Arktisz felett, ami a szélirány megfordulását (zonal wind reversal) eredményezte a 10 hPa szinten. Ez nem csak gyengítette az örvényt, hanem megnyitotta az utat a hideg arkticus levegő délre áramlásához.
Történt-e SSW?
Igen, egy új SSW eseményt detektáltak január elején, amely január közepére (kb. január 14–17. körül) tetőzött. Ez egy rendkívül erős januári esemény, szakértők szerint az egyik legerősebb az elmúlt években. A poláris örvény nyújtása (stretching) és zavarása már megfigyelhető, ami a QBO (Quasi-Biennial Oscillation) keleti fázisa miatt periodikusan ismétlődhet.
Az SSW esemény az Arktisz és Eurázsia felett zajlik, beleértve a szibériai régiót is, ahol a stratoszférikus melegedés hozzájárulhat a felszíni hideg anomáliákhoz. Történelmileg ilyen események gyakran érintik Szibériát, de a jelenlegi fókusz az általános poláris örvény zavarásán van.
Közeli jövőben lehetséges-e újabb SSW?
Igen, a modellek (pl. ECMWF ensemble) szerint január végére (kb. január 25–31.) egy még erősebb zavarás várható, ami újabb SSW-t vagy a jelenlegi esemény meghosszabbítását okozhatja. Ez február elejéig tarthat, és további hideg kitöréseket hozhat. A gyengülő örvény miatt a kockázat magas, különösen a La Niña háttér miatt, ami növeli az SSW valószínűségét (60–75%-kal). Az AO (Arctic Oscillation) negatív marad, ami kedvez a további zavaroknak.
Kilátások az Európai és Kárpát-medencei Télre (2025/2026)
A tél összességében hidegebb az átlagosnál a La Niña és a gyenge poláris örvény miatt, ami dinamikus mintákat hoz: hideg kitörések váltakoznak enyhébb időszakokkal. Az SSW hatása 10–30 nappal később jelentkezik a felszínen, növelve a hideg extrémumok esélyét. Észak-Amerika mellett Európa is érintett, különösen januárban és februárban.
Kárpát-medence (Közép-Európa, pl. Magyarország, Ausztria, Lengyelország) Specifikus Kilátások:
A régió érzékeny az SSW hatására: hidegebb anomáliák januárban, keleties áramlás miatti hideg beáramlás (-10 °C alatti minimumok). December vége óta dinamikus, de januárban hidegebb és havasabb, mint az átlag.
Hőmérséklet:
Januárban kissé hidegebb (anomália -1–3 °C), februárban átlagos vagy enyhébb. Hideg kitörések január végén, február elején.
Csapadék és Hó:
Növekvő hóesés januárban, tartós hótakaró esélye magas (10–20 cm, 7+ nap). Szárazabb február, de hóviharok lehetségesek.
Legfrissebb fejlemények (2025. november 25.)
Jelenleg egy rekord korai SSW esemény zajlik november végén, amely az egyik legkorábbi a megfigyelések történetében (csak a harmadik ilyen az elmúlt 70 évben novemberben). A poláris örvény deformálódása már megkezdődött, a csúcs november 25. körül várható, és a hatások 2–3 héten belül, december elején jelentkezhetnek. Ez a jelenség elsősorban Észak-Amerikát érinti kezdetben, de Európára is hatással lesz, különösen késő decemberben. A La Niña jelenség tovább erősítheti a hideg trendeket, de a stratoszferikus változások dominálnak.
Hatások Európára és Közép-Európára a 2025/2026-os télre
Az előrejelzések vegyesek, de összességében hidegebb és változékonyabb telet várnak, mint amit korábban prognosztizáltak. A svájci MeteoSwiss óvatosságra int: bár a poláris örvény gyengül, a hatások nem feltétlenül terjednek le a felszínre, és az európai tél enyhébb maradhat, mint az "évszázad telel" spekulációk sugallják. Decemberben kicsi a hideg tél valószínűsége, januártól pedig az átlag feletti hőmérséklet várható .
Hőmérséklet-előrejelzések december:
Normál vagy hidegebb az átlagnál Nyugat- és Közép-Európában (pl. Svájc, Németország, Lengyelország), keleties hideg áramlás miatt. Késő decemberben "Kelet fenevadja" (Beast from the East) típusú hideg hullám lehetséges, ami -10 °C alatti értékeket hozhat Közép-Európába. Január: Semleges vagy kissé hidegebb Közép-Európában, szárazabb, hűvösebb levegővel a magasnyomás miatt.Február: Általában melegebb az átlagnál az egész kontinensen, de hidegebb kezdet vagy vég lehetséges.
Csapadék és havazás
december: Növekvő hótakaró Nyugat- és Közép-Európában, jelentős havazás várható a hideg levegő beáramlásával.Január: Alacsonyabb csapadékmennyiség, szárazabb körülmények.Február: Átlagos csapadék Közép- és Nyugat-Európában, több eső/hó az északi részeken.
Regionális fókusz – Közép-Európa (pl. Svájc, Ausztria, Magyarország, Lengyelország):Hidegebb anomáliák decemberben, keleties áramlás miatti hideg beáramlás. A poláris örvény összeomlása főként Észak-Amerikát érinti kezdetben, de Európában enyhébb nyugati áramlás után december végére erősödik a hideg. Történelmi példák (pl. 1958, 1968-as SSW-k) hasonló korai eseményeknél gyengébb hűtést mutattak Észak-Közép-Európában, de a mostani eset erősebb lehet.
Friss X (korábbi Twitter) posztok és vélemények Az X-en is élénk a vita:
A Ventusky figyelmeztet a korai SSW-re, ami hideg arkticus levegőt hozhat Európába, Észak-Amerikába és Ázsiába.Mark Vogan meteorológus élő adásban tárgyalta a hideg, havas Nyugat-Európát.Francia források (CATastrophesNATurelles) megerősítik a hidegebb telet Európában december végéig.
SSW Státusz Frissítés (2026. január 17.)
A legfrissebb adatok alapján (pl. ECMWF, GFS modellek és meteorológiai elemzések) egy aktív Sudden Stratospheric Warming (SSW) esemény zajlik 2026 januárjában. Ez egy major (jelentős) SSW, amely a poláris örvény (polar vortex) erős zavarát okozza, és már január közepén tetőzött. A stratoszférában a hőmérséklet-anomáliák +25–50 °C-os emelkedést mutatnak az Arktisz felett, ami a szélirány megfordulását (zonal wind reversal) eredményezte a 10 hPa szinten. Ez nem csak gyengítette az örvényt, hanem megnyitotta az utat a hideg arkticus levegő délre áramlásához.
Történt-e SSW?
Igen, egy új SSW eseményt detektáltak január elején, amely január közepére (kb. január 14–17. körül) tetőzött. Ez egy rendkívül erős januári esemény, szakértők szerint az egyik legerősebb az elmúlt években. A poláris örvény nyújtása (stretching) és zavarása már megfigyelhető, ami a QBO (Quasi-Biennial Oscillation) keleti fázisa miatt periodikusan ismétlődhet.
Az SSW esemény az Arktisz és Eurázsia felett zajlik, beleértve a szibériai régiót is, ahol a stratoszférikus melegedés hozzájárulhat a felszíni hideg anomáliákhoz. Történelmileg ilyen események gyakran érintik Szibériát, de a jelenlegi fókusz az általános poláris örvény zavarásán van.
Közeli jövőben lehetséges-e újabb SSW?
Igen, a modellek (pl. ECMWF ensemble) szerint január végére (kb. január 25–31.) egy még erősebb zavarás várható, ami újabb SSW-t vagy a jelenlegi esemény meghosszabbítását okozhatja. Ez február elejéig tarthat, és további hideg kitöréseket hozhat. A gyengülő örvény miatt a kockázat magas, különösen a La Niña háttér miatt, ami növeli az SSW valószínűségét (60–75%-kal). Az AO (Arctic Oscillation) negatív marad, ami kedvez a további zavaroknak.
Kilátások az Európai és Kárpát-medencei Télre (2025/2026)
A tél összességében hidegebb az átlagosnál a La Niña és a gyenge poláris örvény miatt, ami dinamikus mintákat hoz: hideg kitörések váltakoznak enyhébb időszakokkal. Az SSW hatása 10–30 nappal később jelentkezik a felszínen, növelve a hideg extrémumok esélyét. Észak-Amerika mellett Európa is érintett, különösen januárban és februárban.
Kárpát-medence (Közép-Európa, pl. Magyarország, Ausztria, Lengyelország) Specifikus Kilátások:
A régió érzékeny az SSW hatására: hidegebb anomáliák januárban, keleties áramlás miatti hideg beáramlás (-10 °C alatti minimumok). December vége óta dinamikus, de januárban hidegebb és havasabb, mint az átlag.
Hőmérséklet:
Januárban kissé hidegebb (anomália -1–3 °C), februárban átlagos vagy enyhébb. Hideg kitörések január végén, február elején.
Csapadék és Hó:
Növekvő hóesés januárban, tartós hótakaró esélye magas (10–20 cm, 7+ nap). Szárazabb február, de hóviharok lehetségesek.
Korábban nem akartam én annyira bele menni az idei tél latolgatásába és a jelenlegi helyzet lefolyásának lehetséges alakulásába, de a szaporodó jelek hatására csak leütöm a (képzeletbeli) azttattt. Ha más nem..
Nézzük a folytatást:
Jelenleg tőlünk messze keletre, északkeletre masszív hidegöblítés zajlik a Kelet-Európai síkság felett. Mindez intő jel arra nézve, hogy eddigi eseménytelen időjárásunkat alakító magasnyomás inkább elodázta sem mint gyengítette a hideget északon.
S, hogy mi vár ránk 2025/2026-os télen?
Még nem tudom, de az novemberi regionális télies epizódot követően (és tartom az időpontot) Karácsony és Szilveszter között lehet ez lehet az idei tél következő dobása. - személyem szerint elméletileg.
- személyem szerint elméletileg.
A jelenlegi körülmények még nem indokolják egyértelműen a makroszinoptikus váltást, de a következő szög az egyhangúság koporsójába a 24-72 óra múlva lezajlódó illetve nagy eséllyel bekövetkezendő Ibériai félsziget felett lefűződő teknő igazolja.
Ez se lenne akkora volumenű jel, de nem mindegy oda miként érkezik hidegöblités.
(Általában tél végére jellemző és zonális teleken, hogy arra felé hamarabb esik hó mint idehaza, persze az ottani magasabb tengerszint feletti magasság sokat segít azon, hogy arra havazzon. Viszont: )
Ez a helyzet nem az a helyzet lesz, amikor bődületes ciklongyár miatt hidegöblités kapnak, hanem inkább az Atlanti - óceánon tanyázó téritő anticiklon meggyengülése miatt.
Nincs két egyforma hidegöblités.
S igy elkövetkeztünk a "tapogatózás birodalmába" jelenleg nem a klasszikus 168 órától < x nem látjuk mi lesz ebből, hanem ha jól lövöm be jó már 144 óránál borul a kép (,mikor lesz ebből tél Európában ezen belül Magyarországon). Ha nem is klasszikus havas, hanem valami száraz lábas vagy valami. A nagy része erősen űridőben van. A lábas hideget nem véletlenül említem nem néz ki úgy hogy az izlandi ciklongyár beadná az unalmast, sőt mostanában még erősödni is fog.
A NAO index korrelációs területei felett a hónap második felében nulla közeli illetve kicsivel az alatti mínusz jöhet. Meglátjuk mire lesz elég. Szerintem az idei tél következő dobása "nehéz szülés lesz", közel sem biztos, hogy amit 144 órától ad, úgy lesz a helyzet lefolyása. Nagyon hamar átcsaphatunk klasszikus Brit blockingba és akár pont karácsony elé vagy a napján ránk kerülhet a hideg vagy a keveredési zóna.
És ugyanez fordítva, hiába a jelentős -15 és -20 fokos sarki hidegmag széle, ami Barents-tengeren át húzódik az Urálig mint ami 144 óránál arra vár(lásd kiragadott beillesztett kép) , hogy bebocsájtást nyerjen mélyen Európába. De mi lesz ha nincs meg a megfelelő anticiklon vagy mély ciklon a megfelelő helyen és időben? Nehéz szülés és kínlódás. Épp ezért látjuk, az alagút végét, de hogy milyen makroszinoptikus felállást kapunk a nyakunkba az még nem látszik. Csúszó pályán érkező atlanti ciklonok bömböm Skandi Ac miatt vagy valami egészen mást, ez később fog kiderülni...
Nem látjuk egyértelműen mi lesz ebből, de hajazok rá hogy valami száraz hidegöblítés lesz vagy klasszikus lábas hideg. Utóbbi esetén legalább keményen fagyna és sütne nap. Már az is valami a kártevőknek, amúgy is belekényelmesedtek az elmúlt évek mediterrán jellegű unalmas teleibe.

Nézzük a folytatást:
Jelenleg tőlünk messze keletre, északkeletre masszív hidegöblítés zajlik a Kelet-Európai síkság felett. Mindez intő jel arra nézve, hogy eddigi eseménytelen időjárásunkat alakító magasnyomás inkább elodázta sem mint gyengítette a hideget északon.
S, hogy mi vár ránk 2025/2026-os télen?
Még nem tudom, de az novemberi regionális télies epizódot követően (és tartom az időpontot) Karácsony és Szilveszter között lehet ez lehet az idei tél következő dobása.
A jelenlegi körülmények még nem indokolják egyértelműen a makroszinoptikus váltást, de a következő szög az egyhangúság koporsójába a 24-72 óra múlva lezajlódó illetve nagy eséllyel bekövetkezendő Ibériai félsziget felett lefűződő teknő igazolja.
Ez se lenne akkora volumenű jel, de nem mindegy oda miként érkezik hidegöblités.
(Általában tél végére jellemző és zonális teleken, hogy arra felé hamarabb esik hó mint idehaza, persze az ottani magasabb tengerszint feletti magasság sokat segít azon, hogy arra havazzon. Viszont: )
Ez a helyzet nem az a helyzet lesz, amikor bődületes ciklongyár miatt hidegöblités kapnak, hanem inkább az Atlanti - óceánon tanyázó téritő anticiklon meggyengülése miatt.
Nincs két egyforma hidegöblités.
S igy elkövetkeztünk a "tapogatózás birodalmába" jelenleg nem a klasszikus 168 órától < x nem látjuk mi lesz ebből, hanem ha jól lövöm be jó már 144 óránál borul a kép (,mikor lesz ebből tél Európában ezen belül Magyarországon). Ha nem is klasszikus havas, hanem valami száraz lábas vagy valami. A nagy része erősen űridőben van. A lábas hideget nem véletlenül említem nem néz ki úgy hogy az izlandi ciklongyár beadná az unalmast, sőt mostanában még erősödni is fog.
A NAO index korrelációs területei felett a hónap második felében nulla közeli illetve kicsivel az alatti mínusz jöhet. Meglátjuk mire lesz elég. Szerintem az idei tél következő dobása "nehéz szülés lesz", közel sem biztos, hogy amit 144 órától ad, úgy lesz a helyzet lefolyása. Nagyon hamar átcsaphatunk klasszikus Brit blockingba és akár pont karácsony elé vagy a napján ránk kerülhet a hideg vagy a keveredési zóna.
És ugyanez fordítva, hiába a jelentős -15 és -20 fokos sarki hidegmag széle, ami Barents-tengeren át húzódik az Urálig mint ami 144 óránál arra vár(lásd kiragadott beillesztett kép) , hogy bebocsájtást nyerjen mélyen Európába. De mi lesz ha nincs meg a megfelelő anticiklon vagy mély ciklon a megfelelő helyen és időben? Nehéz szülés és kínlódás. Épp ezért látjuk, az alagút végét, de hogy milyen makroszinoptikus felállást kapunk a nyakunkba az még nem látszik. Csúszó pályán érkező atlanti ciklonok bömböm Skandi Ac miatt vagy valami egészen mást, ez később fog kiderülni...
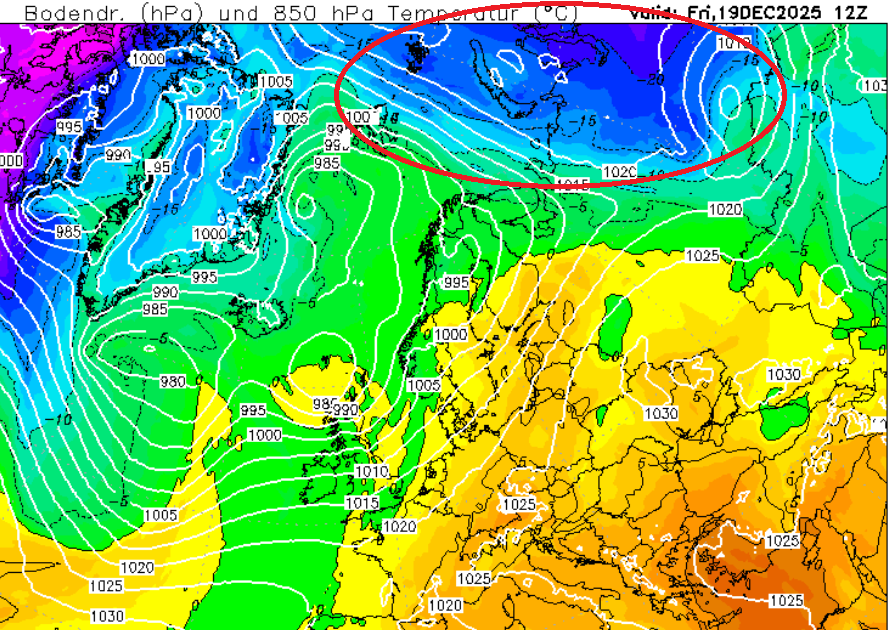
Nem látjuk egyértelműen mi lesz ebből, de hajazok rá hogy valami száraz hidegöblítés lesz vagy klasszikus lábas hideg. Utóbbi esetén legalább keményen fagyna és sütne nap. Már az is valami a kártevőknek, amúgy is belekényelmesedtek az elmúlt évek mediterrán jellegű unalmas teleibe.
Igen, ott már valami kezd látszani.  Egyenlőre nagyon messze van.
Egyenlőre nagyon messze van.  A félblocktól kezdve az Ac által keltett északkeleti oldalzsebes lábas beszivárgásig minden lehet. Valószínűleg a csapadék továbbra is hiánycikk marad, talán annyi változásban reménykedem Szilveszter felé közeledve két ünnep közt, hogy nem lesz ez a "takony idő".
A félblocktól kezdve az Ac által keltett északkeleti oldalzsebes lábas beszivárgásig minden lehet. Valószínűleg a csapadék továbbra is hiánycikk marad, talán annyi változásban reménykedem Szilveszter felé közeledve két ünnep közt, hogy nem lesz ez a "takony idő".
Inger szegény időszak van mostanában.
Amúgy: Üdv nektek, újra Metnet!
Majdnem egy hónapja nem jártam erre.
Inger szegény időszak van mostanában.
Amúgy: Üdv nektek, újra Metnet!
Majdnem egy hónapja nem jártam erre.
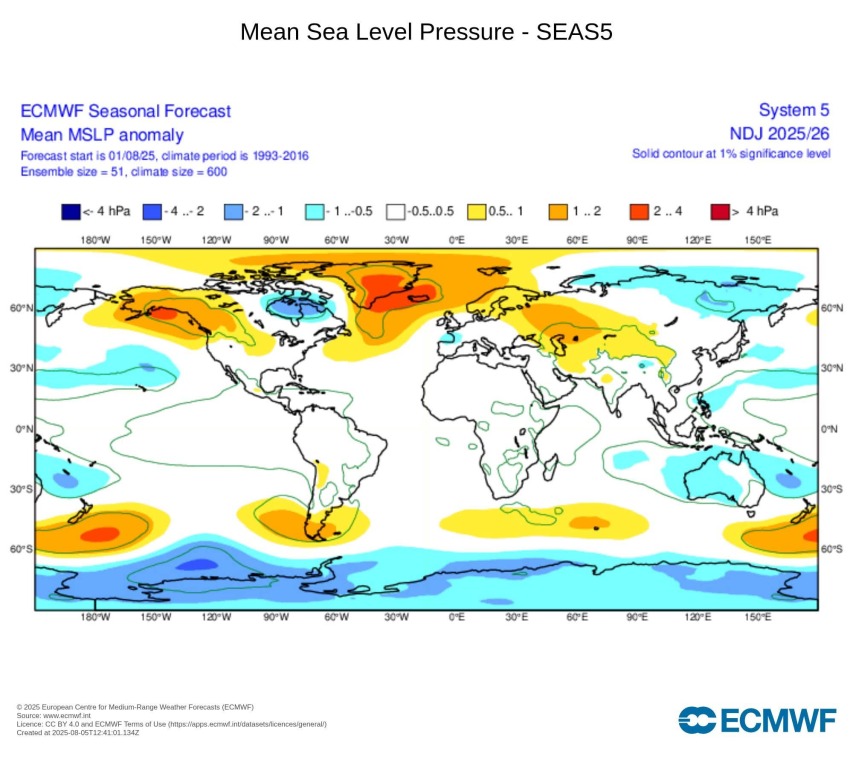
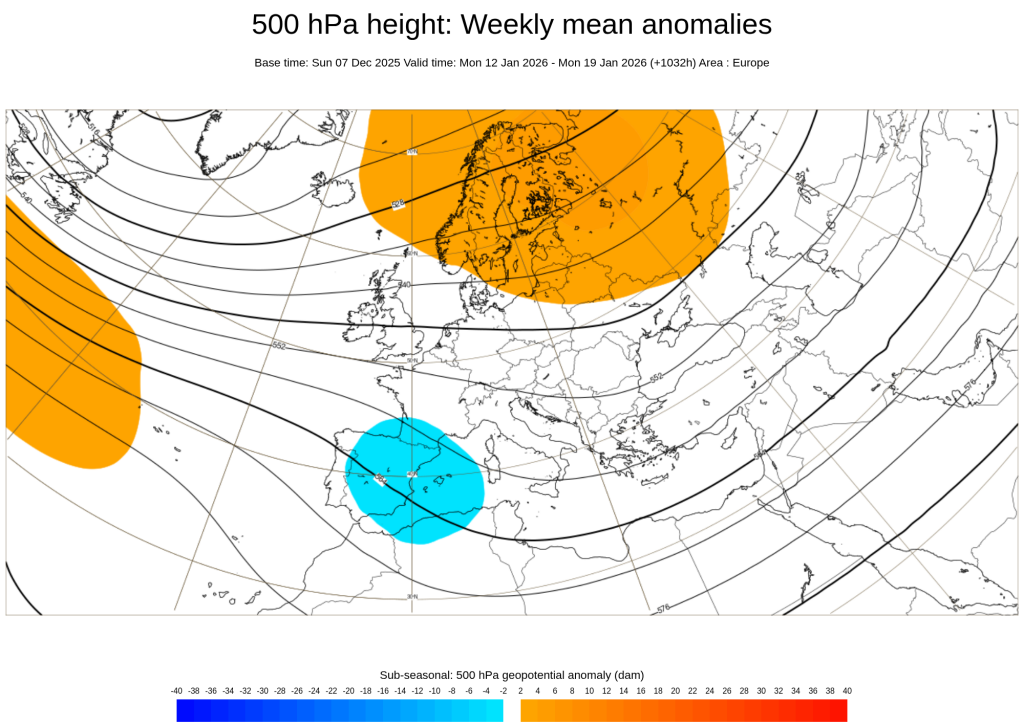
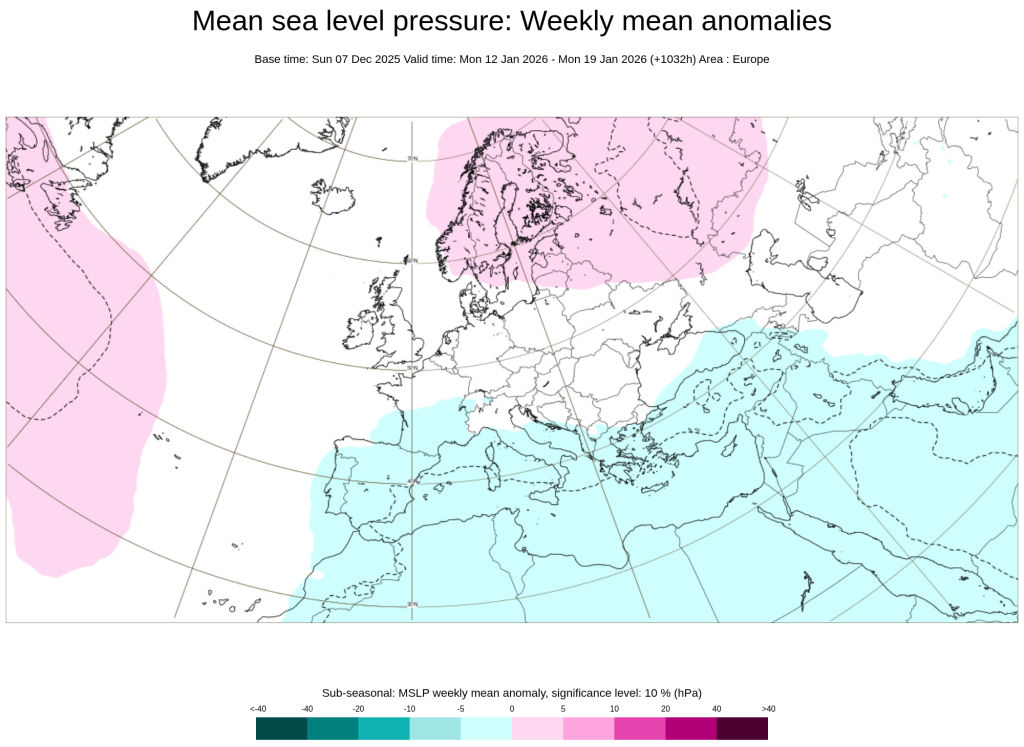
Abszolút nem tartom magam hozzáértőnek, sokkal inkább tanulónak, de az ECMWF heti anomália előrejelzésében azért találtam egy kis reménykeltő dolgot (ha már máshol semmi nincs). Január közepére szerinte inkább a skandináv-északorosz AC-nek állhat a zászló, a Mediterráneumban pedig inkább az alacsonynyomásnak. Ráadásul zsinórban ez a 3. futás, ami hasonló felállást ad.
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
Egy-két gondolat a jelen helyzetről:
A december első dekádja egy rakás...., ismét erős kezdés után. November 19-30 közt nálam a Tmed +0,9°C volt, ami az utóbbi években januárban is ritkaság volt. A makro egyébként tragikusnak tűnik. Az amcsikra kb a fél hidegmag rászakad, -20, -25 fokos izotermák közlekednek a kontinensen, amit Európa hosszú évek óta nem látott. Ez a hideg az óceánra szakadva szteroidon hízlalt csigákat nevel. Ezek nem jutnak be a kontinense, mert a keleti ac, illetve az azori ac gátolja, ez sokat ment a helyzeten, illetve jó előjelnek tartom. Két összekapcsolódó anticiklon, amelyeket erős ciklonok sem tolnak odébb.
Az AO nagyon durván szór, viszont a 10 hepás szél ismét gyengülni fog, ami kérdés, hogy milyen hatással lesz ránk. A modelleken futások óta megjelenik egy felmelegedés, ami akár 40°C is lehet, illetve egyes futásokon az örvény ketté is szakad. Ez is rejt izgalmakat, de szerintem maximum december 25 után lehet bármi hatása ránk.
Ebből a helyzetből kiutat valamilyen formában 20-a körül pedzegetnek a modellek. Szerintem érdemi makrováltás itt úgy lehetne, ha egy ciklon be tudna törni a kontinensre, mögötte pedig a hátoldali -10 fok körüli légtömeg kellően erős enticiklont hozna létre, ami az északra orrosodni hajlamos anticiklonnal és/vagy az észak-orosz anticiklonnal közös, zárt izobárokat hozna létre és lezárnák a nyugati légpályát. Ha ez megtörténik, akkor jöhet érdemi változás, addig marad az októberi hőmérsékletű stratus.
A december első dekádja egy rakás...., ismét erős kezdés után. November 19-30 közt nálam a Tmed +0,9°C volt, ami az utóbbi években januárban is ritkaság volt. A makro egyébként tragikusnak tűnik. Az amcsikra kb a fél hidegmag rászakad, -20, -25 fokos izotermák közlekednek a kontinensen, amit Európa hosszú évek óta nem látott. Ez a hideg az óceánra szakadva szteroidon hízlalt csigákat nevel. Ezek nem jutnak be a kontinense, mert a keleti ac, illetve az azori ac gátolja, ez sokat ment a helyzeten, illetve jó előjelnek tartom. Két összekapcsolódó anticiklon, amelyeket erős ciklonok sem tolnak odébb.
Az AO nagyon durván szór, viszont a 10 hepás szél ismét gyengülni fog, ami kérdés, hogy milyen hatással lesz ránk. A modelleken futások óta megjelenik egy felmelegedés, ami akár 40°C is lehet, illetve egyes futásokon az örvény ketté is szakad. Ez is rejt izgalmakat, de szerintem maximum december 25 után lehet bármi hatása ránk.
Ebből a helyzetből kiutat valamilyen formában 20-a körül pedzegetnek a modellek. Szerintem érdemi makrováltás itt úgy lehetne, ha egy ciklon be tudna törni a kontinensre, mögötte pedig a hátoldali -10 fok körüli légtömeg kellően erős enticiklont hozna létre, ami az északra orrosodni hajlamos anticiklonnal és/vagy az észak-orosz anticiklonnal közös, zárt izobárokat hozna létre és lezárnák a nyugati légpályát. Ha ez megtörténik, akkor jöhet érdemi változás, addig marad az októberi hőmérsékletű stratus.
Néhány gondolat/meglátás a folytatásról a tél kapujában
November utolsó dekádja kifejezetten télies jegyekkel telik, kaptunk havazást, hideget is. A holnap reggel csípős lesz, ismét -5°C köré, alá hűlhet a levegő, majd december elején változás körvonalazódik.
A mediterráneumban kialakult teknő, alacsony geopotenciálú terület fokozatosan feltöltődik, december első pentádjában pedig egyre inkább anticiklon kerül uralomra. Ezzel párhuzamosan messze északon, Alaszkában erős anticiklon fejlődött ki, amely három dolgot eredményez:
1: Észak-Amerika erős hidegbetörsét kap
2: A poláris örvény nem meggyengül, inkább deformálja a magasnyomás, de emiatt az átlag zónaszél rövid időre, de negatívba süllyed 10 hPa-on.Link Ezt átmeneti erősödéss követi, de továbba is gyenge maradhat az örvény, sőt, újabb lassulás jöhet december derekán
3: Az amerikai hideg az óceánra is kijut, amely időszakosan felpörgeti a ciklonokat, amelyek sorozatosan elérik majd Európát. Ezek előoldalán délnyugatról enyhe levegő érkezik.
Ez az enyheség viszont nem a klasszikus délnyugati lángszórónak ígérkezik, hiszen felettünk inkább anticiklonális hatások uralkodnak majd, amely nyugodtabb, kevésbé szeles helyzetet jelent.
Kelet-Európa felett egy jól fejlett maximum épül ki, mely időnként kissé nyugatabbra tolódik. Az azori maximum is terjeszkedik, nem túl magas nyomással, de uralma alá vonja a mediterráneumot. A két maximum időntént zárt izobárokkal egyesül is, ami most semmi érdemit nem okoz, de egy fontos és jó indikátornak tartom a kséőbbiekre nézve, hiszen ha az orosz/szibériai maximum és az azori maximum összekapcsolódik, az vörös szőnyeg a tél előtt.
Az anticiklonális terület a Kárpát-medencére is kiterjed majd, így a ciklonok frontjai csak legyengülve érhetnek el minket, emiatt a mostani csapadékos intermezzo lezárul, szárazabb időszak előtt állunk.
A modellek idelent több napon is kifejezett enyheséget várnak, de hazánk egyik téli ütőkártyája, a hidegpárna ismét közbeszólhat. A jövő hét elejétől egyre nagyobb területet hódíthat meg a stratus, amely várhatóan nem fagyos időt hoz majd, de így is sikerül elkerülni a tizenfokokat, szürke, párás, kora téli idő tűnik a legvalószínűbbnek.
Messze északkeleten eközben Szibériban szépen hízik a hideg, amely nem kifejezetten erős, de domináns maradhat a kanadai maggal szemben.
A NAO december első napjait követően ismét lefelé indul, valamint a fáklyákon is nyílik az olló, így lehetséges, hogy a "csigafelvonulás" utolsó ciklonja mögött az egyébként erre idén kifejezett hajlamot mutató azori anticiklon északra nyúlik és új blokkot épít ki. Ennek a jeleit majd bő egy hét múlva, Mikulás lehet érdemes figyelni, addig marad a nyugodt, szürke, késő őszi/kora téli idő.
November utolsó dekádja kifejezetten télies jegyekkel telik, kaptunk havazást, hideget is. A holnap reggel csípős lesz, ismét -5°C köré, alá hűlhet a levegő, majd december elején változás körvonalazódik.
A mediterráneumban kialakult teknő, alacsony geopotenciálú terület fokozatosan feltöltődik, december első pentádjában pedig egyre inkább anticiklon kerül uralomra. Ezzel párhuzamosan messze északon, Alaszkában erős anticiklon fejlődött ki, amely három dolgot eredményez:
1: Észak-Amerika erős hidegbetörsét kap
2: A poláris örvény nem meggyengül, inkább deformálja a magasnyomás, de emiatt az átlag zónaszél rövid időre, de negatívba süllyed 10 hPa-on.Link Ezt átmeneti erősödéss követi, de továbba is gyenge maradhat az örvény, sőt, újabb lassulás jöhet december derekán
3: Az amerikai hideg az óceánra is kijut, amely időszakosan felpörgeti a ciklonokat, amelyek sorozatosan elérik majd Európát. Ezek előoldalán délnyugatról enyhe levegő érkezik.
Ez az enyheség viszont nem a klasszikus délnyugati lángszórónak ígérkezik, hiszen felettünk inkább anticiklonális hatások uralkodnak majd, amely nyugodtabb, kevésbé szeles helyzetet jelent.
Kelet-Európa felett egy jól fejlett maximum épül ki, mely időnként kissé nyugatabbra tolódik. Az azori maximum is terjeszkedik, nem túl magas nyomással, de uralma alá vonja a mediterráneumot. A két maximum időntént zárt izobárokkal egyesül is, ami most semmi érdemit nem okoz, de egy fontos és jó indikátornak tartom a kséőbbiekre nézve, hiszen ha az orosz/szibériai maximum és az azori maximum összekapcsolódik, az vörös szőnyeg a tél előtt.
Az anticiklonális terület a Kárpát-medencére is kiterjed majd, így a ciklonok frontjai csak legyengülve érhetnek el minket, emiatt a mostani csapadékos intermezzo lezárul, szárazabb időszak előtt állunk.
A modellek idelent több napon is kifejezett enyheséget várnak, de hazánk egyik téli ütőkártyája, a hidegpárna ismét közbeszólhat. A jövő hét elejétől egyre nagyobb területet hódíthat meg a stratus, amely várhatóan nem fagyos időt hoz majd, de így is sikerül elkerülni a tizenfokokat, szürke, párás, kora téli idő tűnik a legvalószínűbbnek.
Messze északkeleten eközben Szibériban szépen hízik a hideg, amely nem kifejezetten erős, de domináns maradhat a kanadai maggal szemben.
A NAO december első napjait követően ismét lefelé indul, valamint a fáklyákon is nyílik az olló, így lehetséges, hogy a "csigafelvonulás" utolsó ciklonja mögött az egyébként erre idén kifejezett hajlamot mutató azori anticiklon északra nyúlik és új blokkot épít ki. Ennek a jeleit majd bő egy hét múlva, Mikulás lehet érdemes figyelni, addig marad a nyugodt, szürke, késő őszi/kora téli idő.
Így kezdődik: "You will see how these stratospheric events will release cold and snow across the United States, Canada, and also Europe, creating a significant pattern change in December and (as currently forecast) also snowfall for the holidays."
Itt azért tényleg van némi szalmaszál pont az ünnepekre, már csak azért is, mert ahogy láttam, azt a pár fokos pozitív anomáliát december első két hetére írja. Mondjuk nagyon jól esne, ha tényleg így lenne.
Itt azért tényleg van némi szalmaszál pont az ünnepekre, már csak azért is, mert ahogy láttam, azt a pár fokos pozitív anomáliát december első két hetére írja. Mondjuk nagyon jól esne, ha tényleg így lenne.
A sztratoszférikus melegedés hatása elég összetett és késleltetett , de nekem erről inkább az jött le, hogy az "első félidő" valóban inkább Amerikának kedvezhet, a másodikban viszont jöhet a "keleti szörny" ide is. Messze nem törvényszerű, de legalább nem olyan eret vágós reménytelenség van, mint az utóbbi minimum 5-7 évben. Nem is bánnám, ha inkább december 2-3. dekádjában alakítana 
Az összes, az oldalon feltüntetett modell előrejelzését kell összeadni és abból egy átlagot vonni. Ez általában bejön. Vagy legalábbis közeledik a valósághoz. Néhány napig koratélies időnk lesz, tiöbb kevesebb csapadékkal, különösebb szélsőségek nélkül.
Ez egyelőre(!) tényleg jó előjel, plusz annyi előnye is van a szibériai hidegmag erősödéséhez hozzájáruló makrofelállásnak, hogy a fenti poláris örvényt ez most segít visszafogni ismét.
Makroszinoptika a többhetesben a köv. hetekre:
Makroszinoptika a többhetesben a köv. hetekre:
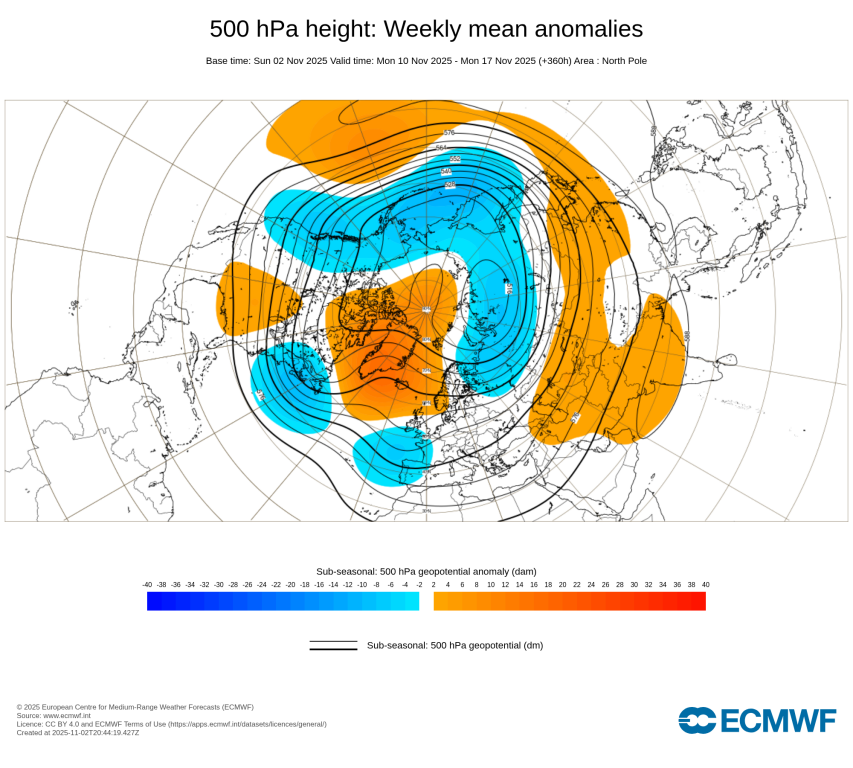
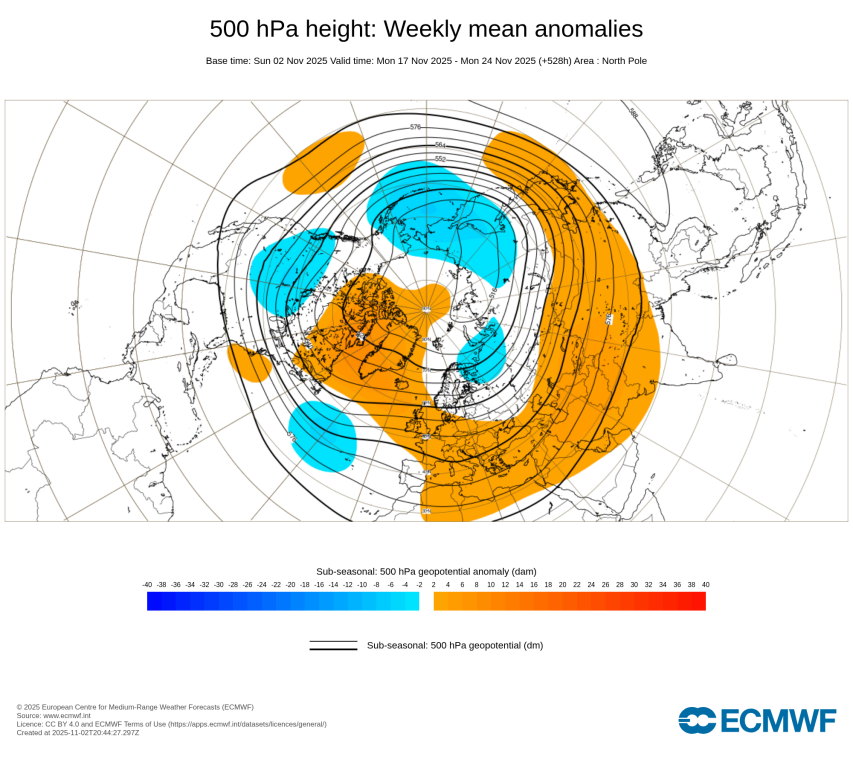
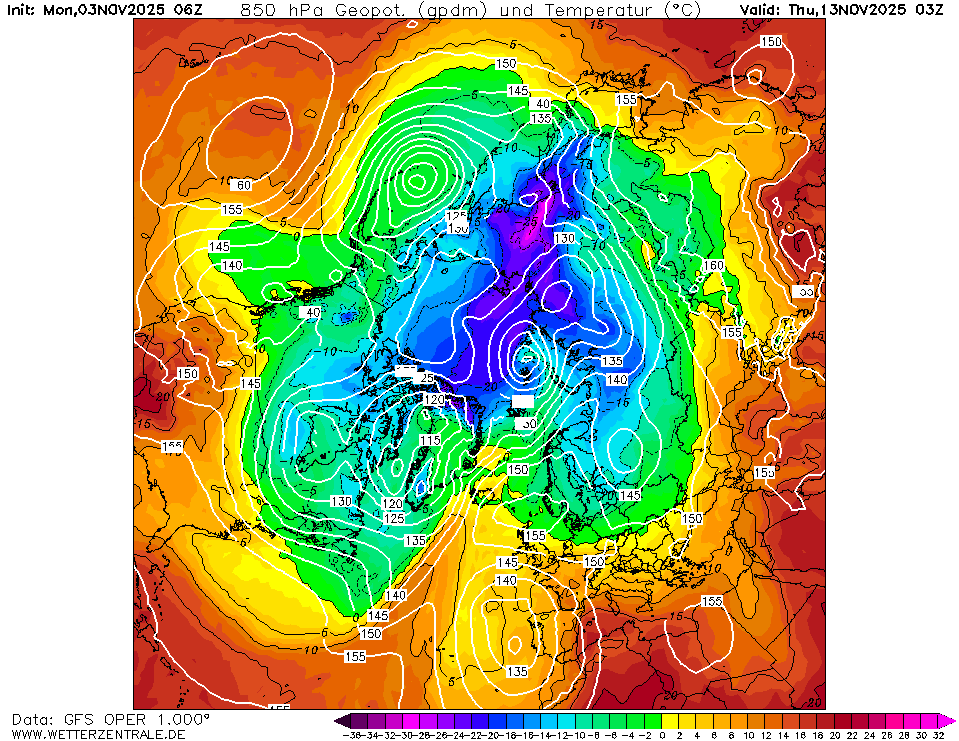
A szibériai hidegdepó csak nő és nő, remélhetőleg mi is kapunk majd belőle hamarosan.
Ami mégjobb kanada környékén egyenlőre elég gyenge a hidegfelhalmozodás.
Tényleg lehet bízni a jó télben.
A hozzászólást a moderátor áthelyezte ide:
- Meteorológiai társalgó (#679730)
Írtam egy latolgatást az idei téli előjelekkel kapcsolatban, melyek szerintem nagyon bíztatóak! Az alábbi linken megtaláljátok. Remélem márciusban végre tényleg hosszú kék oszloppal gyarapszik a téli anomáliák diagramja
A tanulmányban igyekeztem matematikailag is bizonyítani a feltevésem és szerintem bíztató eredmény született
Link
A tanulmányban igyekeztem matematikailag is bizonyítani a feltevésem és szerintem bíztató eredmény született
Link
Link
Egy kis érdekesség, egyre valószínűbb a hidegebb tél!
Tudom ez egy ki ragadott futás, de már régóta ezt adja, és a Szibériai hó felhalmozodás is nagyon magasan van ebben az a hónapban.
Elég nagy befolyással bír az örvényre ha több a hó van ott ilyenkor, sokkal gyengébb lehet az örvény.
Ha ez így folytatódik és a poláris örvény továbbra is gyengélkedik majd, mert így várják, akkor nem lesz bajunk a télen.

Egy kis érdekesség, egyre valószínűbb a hidegebb tél!
Tudom ez egy ki ragadott futás, de már régóta ezt adja, és a Szibériai hó felhalmozodás is nagyon magasan van ebben az a hónapban.
Elég nagy befolyással bír az örvényre ha több a hó van ott ilyenkor, sokkal gyengébb lehet az örvény.
Ha ez így folytatódik és a poláris örvény továbbra is gyengélkedik majd, mert így várják, akkor nem lesz bajunk a télen.
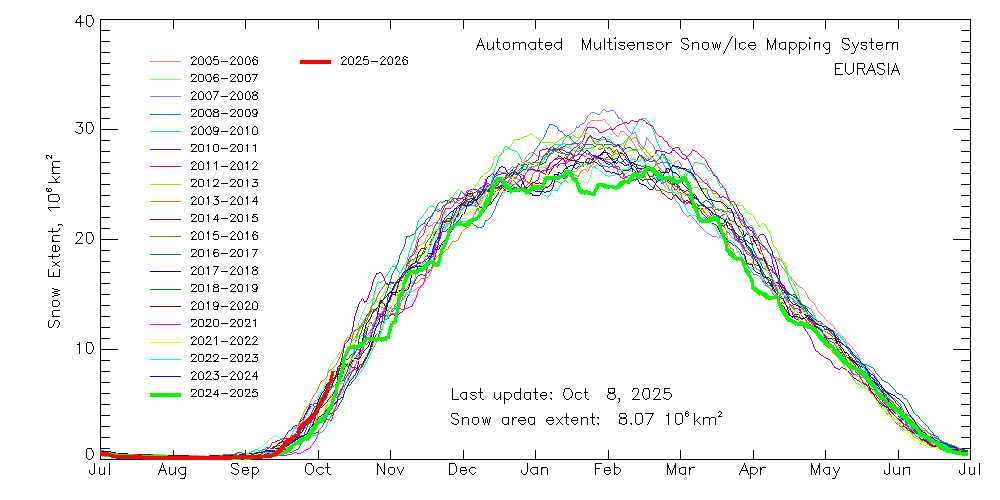
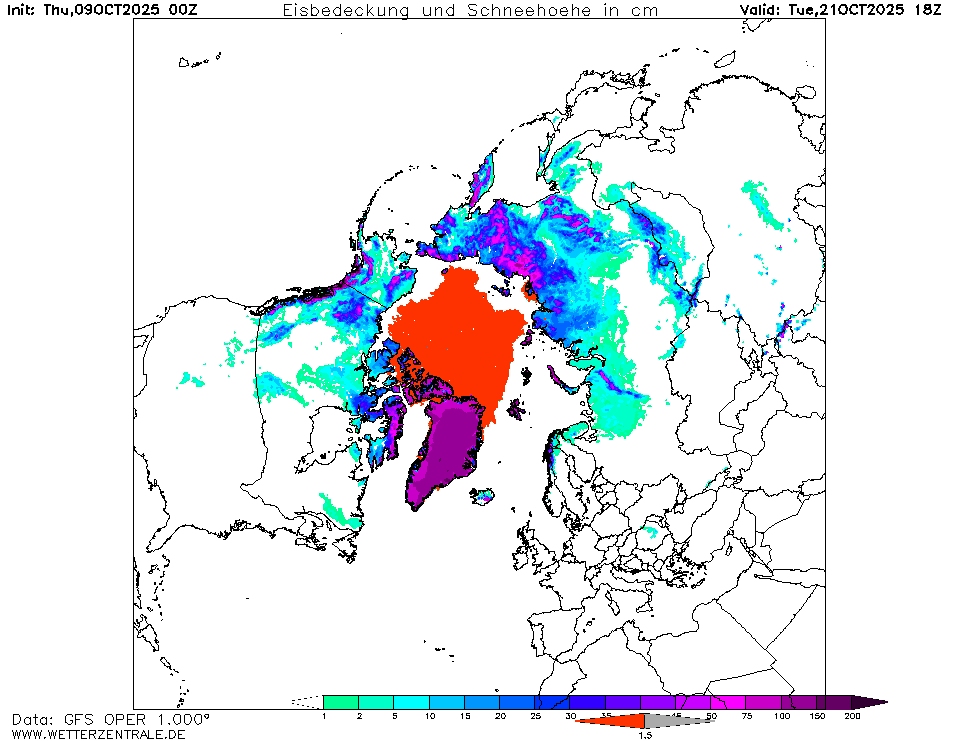
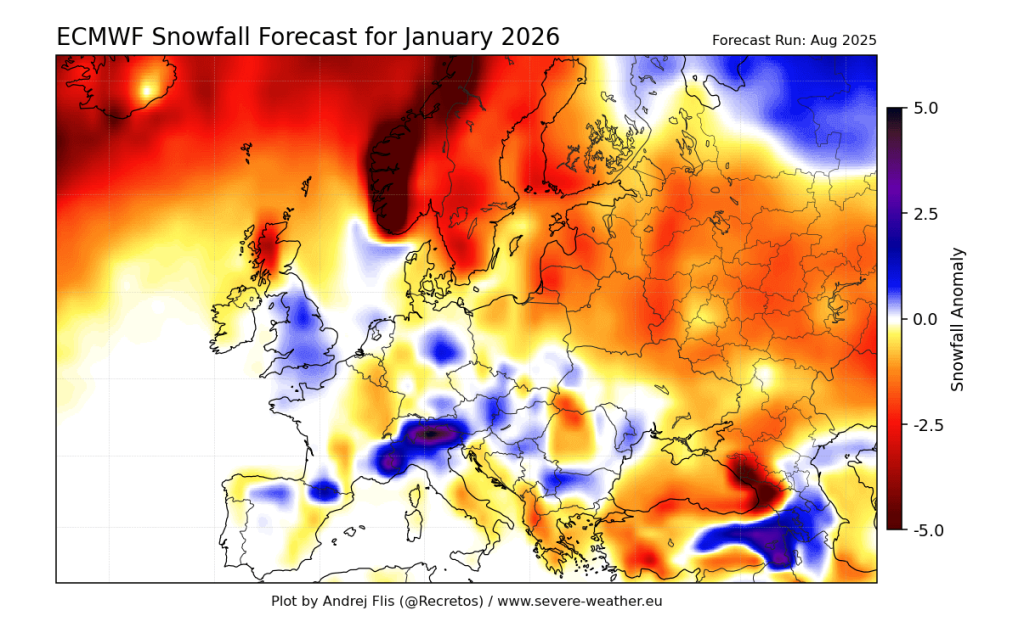
Bízom benne hogy ez a tél más lesz, kijárna már nekünk, egy havas hideg tél.
Itt már azért este hűvösebbek vannak 22 orakor az őrtűz gyújtás 15 fokban indult.
fh:Kézdiszék
fh:Kézdiszék



Tudom, űrtáv, egy kiragadott futás meg minden, de ez durvára sikerült! Néhány másik modell (pl. GFS is) adja gyengébb kivitelben. Augusztus utolsó napjaira tényleg nagy váltás jöhet a makroképben ezzel az exhurrikánnal.
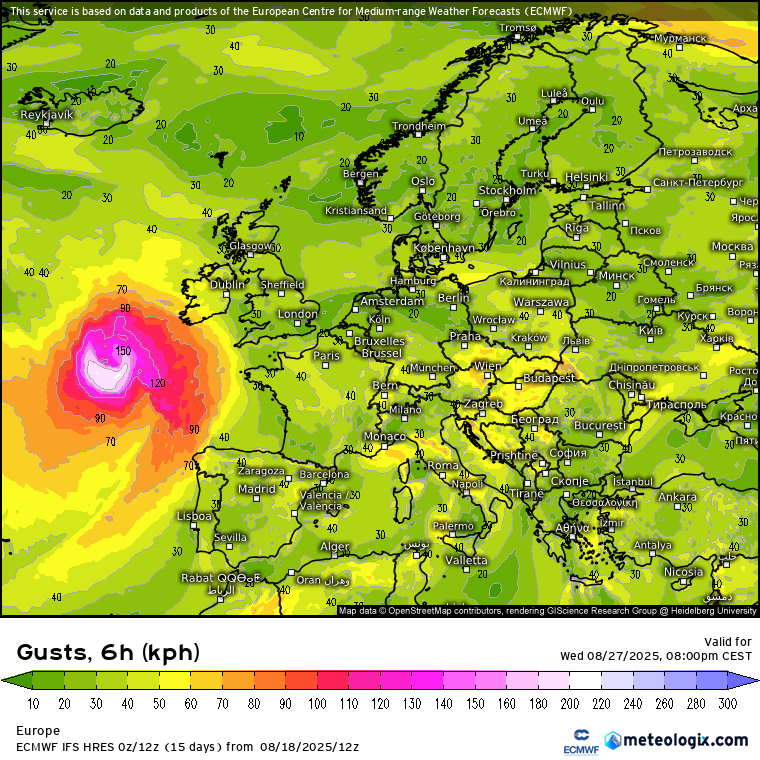
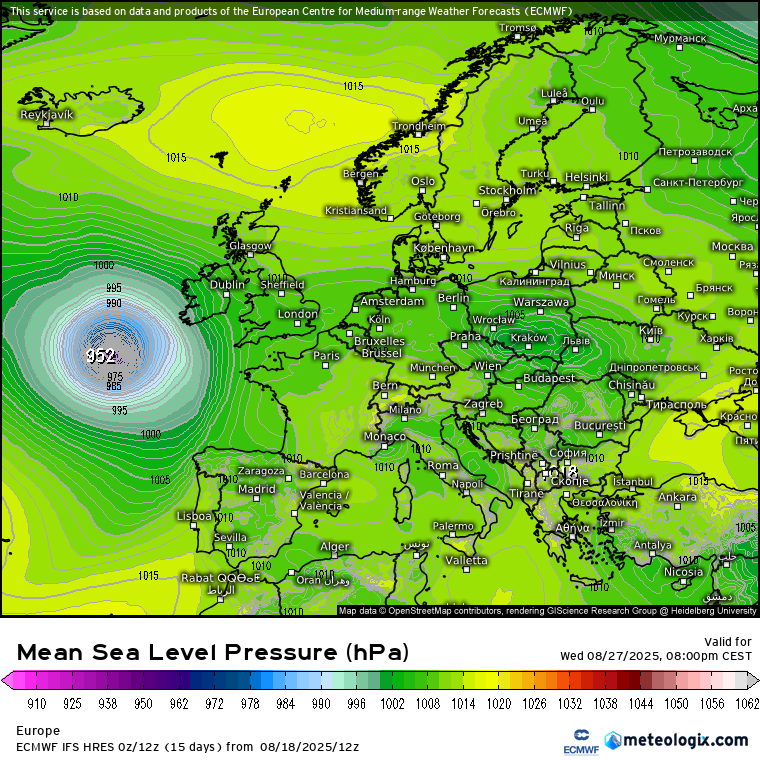
A hőség tartósságát tekintve ez a két hét lett/lesz a nyár legnagyobb dobása, az nem kérdés, de a komolyabb maximumokat ezúttal is meghiúsítják a túl északon elhelyezkedő és a brit-német térségben rendre kiújuló anticiklonok. Ezek első, múlt hétvégén kialakult példánya még gyorsan fölénk helyeződött mostanra, de arra elég volt, hogy kettévágja a forró időszakot. Aztán mire megint jobban fölénk húzódna - a közben azért gyengülő - igen meleg légtömeg nyugatról, addigra újra AC képződés néz ki a Brit-szigetek térségében, ráadásul az már tartósabbnak tűnik, így vasárnaptól legalább pár napig rendes blocking helyzet néz ki, nálunk megint északiasra forduló áramlással. Üröm az örömben, hogy az utóbbi futások alapján sajnos növekszik az esélye, hogy megint gyorsan benyomul fölénk az AC pereme, így a csapadék-kilátások nem túl biztatóak (pedig korábban még több záporos-zivataros nap is benne volt a pakliban).
Az érdekesebb dolgok majd augusztus 20. után jöhetnek, ugyanis az első komolyabb hurrikán, Erin szépen berongyol a nyugati áramlási övbe, nem csoda, hogy lobognak is a fáklyák ott (illetve ettől függetlenül már most vasárnap is megnő a szórás, néhány modell/modelltag határozottabb lehűlést is pedzeget, 10 °C alá csökkenő T850-nel). Egyelőre kétféle verzió tűnik leginkább elképzelhetőnek, vagy áttöri az ex-trópusi ciklon az AC-t és beindulhat valami lájtos, "nyárias" zonalitás-féleség, vagy beleolvad az észak-amerikai/grönlandi cikloncentrumba, és akkor az előoldali meleg áramlás még erősítheti is az AC-t, nálunk tartósabbá téve az északias irányítást.
Az érdekesebb dolgok majd augusztus 20. után jöhetnek, ugyanis az első komolyabb hurrikán, Erin szépen berongyol a nyugati áramlási övbe, nem csoda, hogy lobognak is a fáklyák ott (illetve ettől függetlenül már most vasárnap is megnő a szórás, néhány modell/modelltag határozottabb lehűlést is pedzeget, 10 °C alá csökkenő T850-nel). Egyelőre kétféle verzió tűnik leginkább elképzelhetőnek, vagy áttöri az ex-trópusi ciklon az AC-t és beindulhat valami lájtos, "nyárias" zonalitás-féleség, vagy beleolvad az észak-amerikai/grönlandi cikloncentrumba, és akkor az előoldali meleg áramlás még erősítheti is az AC-t, nálunk tartósabbá téve az északias irányítást.
Most viszont már kijelenthető, hogy ebből végül nem igazán lett semmi, Nyugat-Európában egyáltalán nem, de itt középen is csak pár napig leszünk a teknő előoldalán, utána visszatér az május óta azért többször megújuló északnyugatias irányítás.
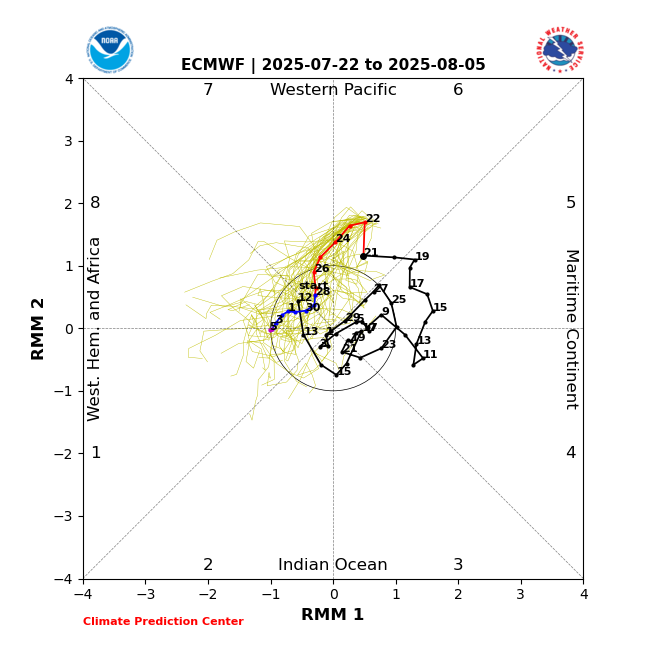
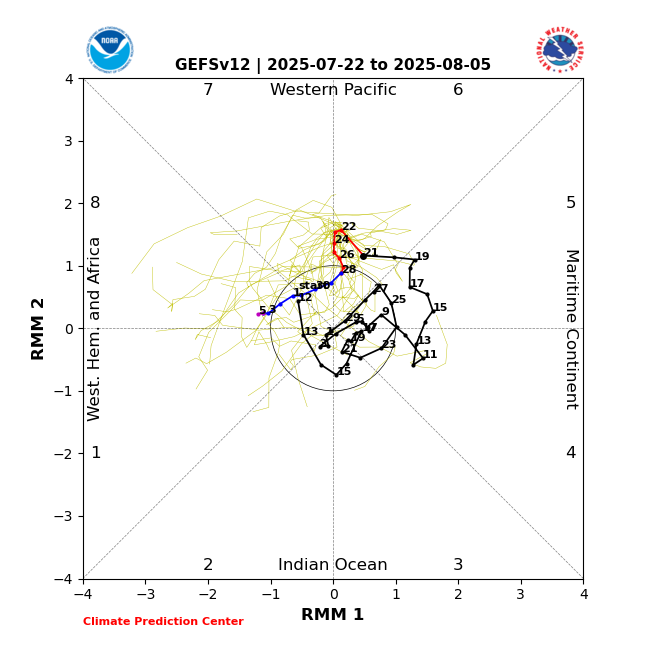
Ez egyébként annyira nem meglepő, mivel elég masszív a szubtrópusi AC öv (nem csoda, hogy idén eddig még egyetlen értelmes trópusi ciklon sem tudott kialakulni az Atlanti-óceánon), illetve északra is húzódott, így a tartósabb nyugat-, délnyugat-európai teknőknek esélyük sincs, a mostanihoz hasonlók is rendre eltolódnak keletebbre. Augusztus elejéig ebben nem is nagyon látszik számottevő változás, de az egész hónapot azért még nem írnám le, már csak azért is, mert a Madden-Julian oszcilláció kedvező fázisba kerülhet a hónap első napjaiban (most épp a Csendes-óceán nyugati részén az, és ott meg is indul a trópusi ciklonok dömpingje), bár abban még elég nagy az eltérés a modellek között, hogy mennyire lesz intenzív és tartós ez a fázis. Mindenesetre ha egy-két hurrikán kialakul, az majd könnyen boríthatja az eddigi stabil légköri helyzetet.
Ez egyébként annyira nem meglepő, mivel elég masszív a szubtrópusi AC öv (nem csoda, hogy idén eddig még egyetlen értelmes trópusi ciklon sem tudott kialakulni az Atlanti-óceánon), illetve északra is húzódott, így a tartósabb nyugat-, délnyugat-európai teknőknek esélyük sincs, a mostanihoz hasonlók is rendre eltolódnak keletebbre. Augusztus elejéig ebben nem is nagyon látszik számottevő változás, de az egész hónapot azért még nem írnám le, már csak azért is, mert a Madden-Julian oszcilláció kedvező fázisba kerülhet a hónap első napjaiban (most épp a Csendes-óceán nyugati részén az, és ott meg is indul a trópusi ciklonok dömpingje), bár abban még elég nagy az eltérés a modellek között, hogy mennyire lesz intenzív és tartós ez a fázis. Mindenesetre ha egy-két hurrikán kialakul, az majd könnyen boríthatja az eddigi stabil légköri helyzetet.

Huszadika után a GFS-en meg is jelent ide 45,1 fok képében. Szuper, alig várom. 
Ott van még sajnos a lehetőség mindig. A “normál” globálikon már fel is tűnt.
Oké, GFS ami szinte mindig felülbecsül, de akkor is.
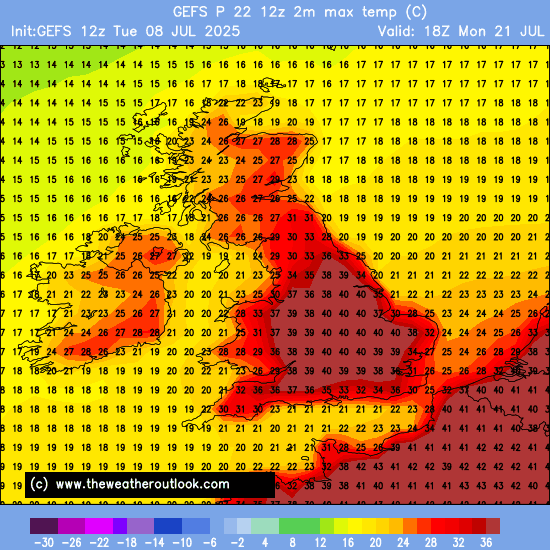
Oké, GFS ami szinte mindig felülbecsül, de akkor is.
És most, hogy látod? Jönni fog az a ciklon? Nekem úgy tűnik, h vmi porszem került a gépezetbe, és jönnek majd a folyamatos özönvízek.
Ma olvastam egy - Nyugat-Európára kihegyezett - esélylatolgatást, mely szerint a felső-troposzférikus jet-ek alapján a Rossby-hullámok egyes forgatókönyvek szerint pont úgy alakulnának, hogy az ABH pont úgy foglalna helyet, hogy engedné az Észak-Atlani AC előoldalán a hidegadvekciót a Földközi-tenger nyugati medencéjébe. Ez ott egy ibériai teknőt hozna létre, ami egy “forró pumpát” csinálna. Az 5-6 fokos pozitív anomáliás tenger felett nagyon gyorsan eljutna Európába a rendkívül meleg szaharai levegő, ami főleg Nyugat-Európában okozhatna extrém meleget, de a ciklon esetleges keletre mozdulásával végigsöpörne a kontinensen. Ez egyébként július 2. felére prognosztizálható “legrosszabb esetként”, amikor a Rossby-hullám felettünk ismét alacsonyabb szélességekre hatolna.
Egy szava nem lehet azoknak, akik szeretik az évszakos átlagnál több fokkal hűvösebb időt és csípőből rühellik a meleget. Jövőhéten is akad majd pár olyan nap, amikor melegebb lesz Moszkvában, mint Budapesten.  A Spanyolok sem fognak fázni, bár az kevésbé meglepő.
A Spanyolok sem fognak fázni, bár az kevésbé meglepő.
A friss Ecm-en a soron következő, már nem számolom hanyadik nyüves hidegfront azért mégis csak behozza a 3 fokos izotermát egy hét múlva péntekre.
Belül ilyenkor azért sírok. Bevallom.
A friss Ecm-en a soron következő, már nem számolom hanyadik nyüves hidegfront azért mégis csak behozza a 3 fokos izotermát egy hét múlva péntekre.
Belül ilyenkor azért sírok. Bevallom.
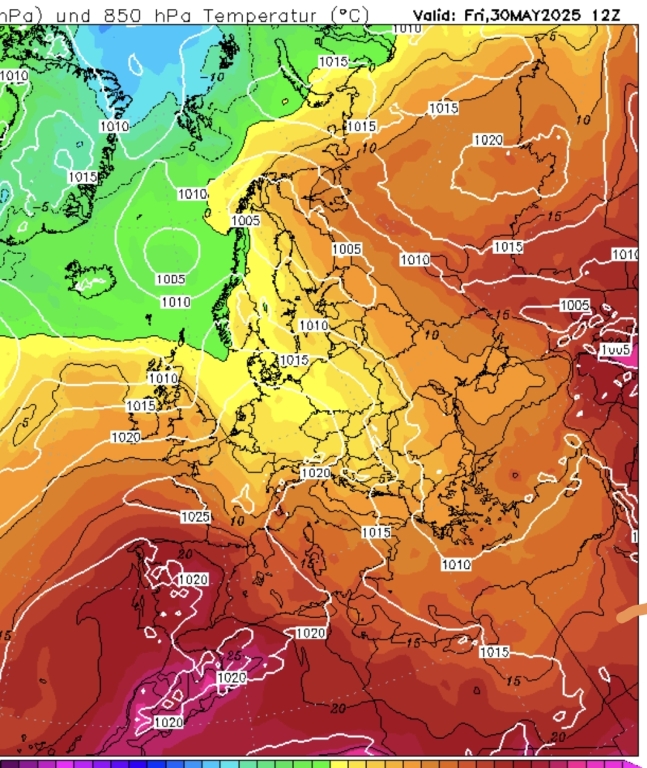
Pár szösszenet...
Összeomlóban a vortex, köszönjük meg neki is a várhatóan csapadékosabb jövő hetet, mivel a vertikális metszeten látszik, az örvény tengelyének belógása K-Európa fölé segíti megállítani a mostani helyzetében az Izland alatti AC-t.
Utána meglátjuk, mi lesz, AC tartósabban visszajön-e vagy más felállások, újabb csapadékos etapok kialakulásával. Amire kíváncsi leszek, az a hónap vége, a gyenge zonális szelek még lejjebb csúsznak-e, addigra helyeződhetne az örvény helyetti magassági AC pont a pólusra, plusz a trópusokról érkező befolyásoló tényezők is blokk felé mutathatnak. Ennek ellentmond, hogy űrtávban nem csökkennek az indexek egyelőre, bár az OP képe alapján csak a futási időn túl lehetnének erre jelek.
Végül pedig egy extrém hosszú kitekintés a nyárra, szigorúan érdekességként az amcsi multimodell korábbi futásainak valószínűségi ábrái a hőmérsékletre. Egyben nézve az egész féltekét, nem kell kommentálni, mennyire siralmas az idei előre. Évszakos beválási esélyeket észben tartva, és a nagyképet figyelve, nem kiragadva az Eu/Észak-Afrika térséget is elég erős.
Összeomlóban a vortex, köszönjük meg neki is a várhatóan csapadékosabb jövő hetet, mivel a vertikális metszeten látszik, az örvény tengelyének belógása K-Európa fölé segíti megállítani a mostani helyzetében az Izland alatti AC-t.


Utána meglátjuk, mi lesz, AC tartósabban visszajön-e vagy más felállások, újabb csapadékos etapok kialakulásával. Amire kíváncsi leszek, az a hónap vége, a gyenge zonális szelek még lejjebb csúsznak-e, addigra helyeződhetne az örvény helyetti magassági AC pont a pólusra, plusz a trópusokról érkező befolyásoló tényezők is blokk felé mutathatnak. Ennek ellentmond, hogy űrtávban nem csökkennek az indexek egyelőre, bár az OP képe alapján csak a futási időn túl lehetnének erre jelek.

Végül pedig egy extrém hosszú kitekintés a nyárra, szigorúan érdekességként az amcsi multimodell korábbi futásainak valószínűségi ábrái a hőmérsékletre. Egyben nézve az egész féltekét, nem kell kommentálni, mennyire siralmas az idei előre. Évszakos beválási esélyeket észben tartva, és a nagyképet figyelve, nem kiragadva az Eu/Észak-Afrika térséget is elég erős.

Klasszikus blockingba fordulás az északi zónázásból?!
Nos úgy tűnik igen és remélhetőleg az előjelek valósak egy igazi, kemény téltámadásnak, melyek felcsillantak a fáklya diagrammokon és már 1-1 operatív futáson is.
Jelenleg Izlandnál és a Spitzbergáktól keletre örvénylik ciklon, melyek együttesen egy rendszert alkotnak, míg delebbre egy hosszan elnyúlo magasnyomású gerinc helyezkedik el, egészen a nyugati ága az Atlanti-óceán fölé nyúlva.
Link
A változás 24 óra múlva el is indul azzal, hogynaz Izlandi ciklon szépen kelet, északkelet felé mozdulva beleolvad a sarkvidéki, igen hideg hőmérséklettel rendelkező magassági teknőbe, majd tovább mélyül és a korábbi ciklon helyébe lép a Jeges-tenger felett, Novaja Zemlja felé közelítve. Grönlandtól nyugatra a változást okozó, igen fontos történés is hamarosan lezajlik. A Baffin-öböl felett és Grönland felett is a következő 48 órában légnyomás emelkedés valószínű és anticiklon telepedik meg az előbbi térség felett. Ez kulcs szerepet játszik a folytatásban! Egy északkelet-délnyugat tengelyű magasnyomás nyúlhat ki az ócean fölé, bár GFS-en erősebb az AC 120 óránál, mint a frissülő ECMWF-en. Ennek a magasnyomásnak a keleti peremén kifejlődő ciklon a Brit-szigeteket elérve gyorsan tovább száguld kelet felé, s szinten beleolvad a markáns Skandináv ciklonrendszerbe. Az Azori-szigeteki ciklon elől a hidegcsapok elzáródnak, győzedelmeskedni látszik a magasnyomás és ezzel vélhetően egy komoly átrendeződés indulhat meg Európa időjárásában a jelenlegi számítások szerint.
144 óránál Amerika keleti partjainál a ciklon bepörög, a Brit ciklon kelet felé helyeződik és megerősödik az anticiklon az Észak-atlanti térségben.
Link
Link
Észak-Európában már jelentős méreket ölt a hideg, mely fokozatosan egyre délebbre jut és Nyugat-Európát is eléri a hideg, ahogyan a magasnyomás kelet felé tolódik a folytatásban.
Innentől azonban megnő a bizonytalanság! A friss számítások szerint most a teljes blockingba fordulás lehetőségét adjákk a modellek. A hideg első hulláma csupán érintőleges lehet és ekkor még komoly téli fordulatra csekélyebb az esély, majd űridős futásban a friss ICON/GFS már totális blockingba fordulást jelez, hiszen Amerika partjai felett a ciklon déli áramlássan megújítaná a blocking északi ágát, s a GFS-en ugyan elkenődne az első AC, de ezzel a kiújuló, újabb Észak-Atlanti blockinggal a teljes télbe fordulás következne be.
Link
Friss ECMWF-en végig erősebben megmaradna a blocking és 192 óránál teljes makrokép váltásra állna át az időjárás
Link
Ettől tovább boncolgatni, feszegetni nem szeretném a helyzetet, még bőven lehet változás. Amennyiben a következő 2-3 (ECMWF) futás középtávon nem változik jelentőset, úgy igen nagy lépést tehetünk, akár egy keményebb fajta, tartós téli idő bekövetkezésére, sok év elteltével... Egyelőre azért durva jelzőket nem használnék, sokszor és sokat koppantunk már, de most mintha napról napra növekedne az esélye egy erősebb, tartósabb téltámadásnak Európában!
Link
Nos úgy tűnik igen és remélhetőleg az előjelek valósak egy igazi, kemény téltámadásnak, melyek felcsillantak a fáklya diagrammokon és már 1-1 operatív futáson is.
Jelenleg Izlandnál és a Spitzbergáktól keletre örvénylik ciklon, melyek együttesen egy rendszert alkotnak, míg delebbre egy hosszan elnyúlo magasnyomású gerinc helyezkedik el, egészen a nyugati ága az Atlanti-óceán fölé nyúlva.
Link
A változás 24 óra múlva el is indul azzal, hogynaz Izlandi ciklon szépen kelet, északkelet felé mozdulva beleolvad a sarkvidéki, igen hideg hőmérséklettel rendelkező magassági teknőbe, majd tovább mélyül és a korábbi ciklon helyébe lép a Jeges-tenger felett, Novaja Zemlja felé közelítve. Grönlandtól nyugatra a változást okozó, igen fontos történés is hamarosan lezajlik. A Baffin-öböl felett és Grönland felett is a következő 48 órában légnyomás emelkedés valószínű és anticiklon telepedik meg az előbbi térség felett. Ez kulcs szerepet játszik a folytatásban! Egy északkelet-délnyugat tengelyű magasnyomás nyúlhat ki az ócean fölé, bár GFS-en erősebb az AC 120 óránál, mint a frissülő ECMWF-en. Ennek a magasnyomásnak a keleti peremén kifejlődő ciklon a Brit-szigeteket elérve gyorsan tovább száguld kelet felé, s szinten beleolvad a markáns Skandináv ciklonrendszerbe. Az Azori-szigeteki ciklon elől a hidegcsapok elzáródnak, győzedelmeskedni látszik a magasnyomás és ezzel vélhetően egy komoly átrendeződés indulhat meg Európa időjárásában a jelenlegi számítások szerint.
144 óránál Amerika keleti partjainál a ciklon bepörög, a Brit ciklon kelet felé helyeződik és megerősödik az anticiklon az Észak-atlanti térségben.
Link
Link
Észak-Európában már jelentős méreket ölt a hideg, mely fokozatosan egyre délebbre jut és Nyugat-Európát is eléri a hideg, ahogyan a magasnyomás kelet felé tolódik a folytatásban.
Innentől azonban megnő a bizonytalanság! A friss számítások szerint most a teljes blockingba fordulás lehetőségét adjákk a modellek. A hideg első hulláma csupán érintőleges lehet és ekkor még komoly téli fordulatra csekélyebb az esély, majd űridős futásban a friss ICON/GFS már totális blockingba fordulást jelez, hiszen Amerika partjai felett a ciklon déli áramlássan megújítaná a blocking északi ágát, s a GFS-en ugyan elkenődne az első AC, de ezzel a kiújuló, újabb Észak-Atlanti blockinggal a teljes télbe fordulás következne be.
Link
Friss ECMWF-en végig erősebben megmaradna a blocking és 192 óránál teljes makrokép váltásra állna át az időjárás
Link
Ettől tovább boncolgatni, feszegetni nem szeretném a helyzetet, még bőven lehet változás. Amennyiben a következő 2-3 (ECMWF) futás középtávon nem változik jelentőset, úgy igen nagy lépést tehetünk, akár egy keményebb fajta, tartós téli idő bekövetkezésére, sok év elteltével... Egyelőre azért durva jelzőket nem használnék, sokszor és sokat koppantunk már, de most mintha napról napra növekedne az esélye egy erősebb, tartósabb téltámadásnak Európában!
Link
Téli kitekintések: Egyéni ünnepi kiadásom
Egy kicsit nehezen kezdem szavaim, szerintem idén nem is nagyon latolgattam a telet. "Nem volt mit, mi kiverje az ingerküszöbömet." Hosszú hallgatásomat megtörve, a mostani helyzetből igaz sikerült egy átmeneti 2-3 cm vizes tapadós latyakot összehoznunk az elmúlt 3 napban, ami tegnapra jócskán megfogyatkozott.
Hosszú hallgatásomat megtörve, a mostani helyzetből igaz sikerült egy átmeneti 2-3 cm vizes tapadós latyakot összehoznunk az elmúlt 3 napban, ami tegnapra jócskán megfogyatkozott.
Mostanra a GFS kacérkodik "utolsó szalmaszálként" Karácsony utánra némi havacskával.
Jelenlegi GFS alapján Tisza vonalában érkezne észak felől. December 27-én hajnalban illetve reggel:
December 27-én hajnalban illetve reggel:
A hosszútávú topik témájánál maradva a változékonyság jelei űridőben már tapasztalhatók. (Erről később lentebb.) A GFS rendületlenül adja üveggömb tartományban (még) 192 órán túl < x időpontokban. (Úgy fest jó lesz egy életre megjegyeznem, hogy a a gyenge La Nina egyúttal kedvezhet is a jobb télnek mint sem egy erősebb.)
A markánsabb változás európai jelei már 192 órán belülre értek, aminek hazánkra gyakorolt hatása napról napra nő és ennek folyományaként amatőr latolgatóként január első dekádjára de leginkább nagyjából jan 2 ás jan 10 közé klasszikus Brit Blockingot vagy annak egyéb blockoló Brit Izlandi Ac-t valószínűsítek, hozzánk pedig ényi áramlást.
(Azon belül már csak részlet kérdése, hogy ha itt landol a hideg hogy sikerül medi? hf? csapdék? halmazállapot? területi lefedettség? Ez 144 órán belüli történet, amibe jóslásba most nem bocsátkoznék. )
)
Bővebben, adatokba kapaszkodva:
A mostani makrokép is nagyjából meridionális, attól függetlenül hogy nincs még hideg, illetve nincs a közelben elegendő, amit letud forgatni hozzánk. A csapadék is adott, csak a hideg hiányzik. Ami pedig ilyenkor lenni szokott, hogy ezt általában félzónás, zónás jegyek követik. Ha csak az ECM lapozom végig északi zónalitás-> félblock - > megint északi zóna. Ha a GFS -t nagyjából hasonló helyzet.
A régi metnetes öregektől 2010 előtti és alatti időben mindig azt tanultam, hogy az északi zóna egy fokkal jobb makroszinoptikai helyzet mint a sima zóna, mert előbbi esetén nem pucolódik ki a hidegbázis Európa közeléből, ami 5-6 napos távban blockba le is tud fűződni, ha akad egy Rossby hullám amit meglovagol avagy lefűződik nahh, akár a mi szélességünkre. Másik érv az északi zóna mellett, hogy viszonylag egyben tartja a hidegbázist Európára néző felén.
A változás pedig elég szembeötlően ott van szakavatott amatőr vagy hivatalos szemeknek, mivel mindkét nagy "királyi" modell / GFS, ECMWF / nagyjából egyetért, hogy 144 órától ( dec.29) Izland és attól északra elhelyezkedő vizek felett tartósan megveti magát a 850hPalon vett ~1550m () -10 - (-15) fok körüli légtömeg. (Az ottani stabil Grönlandi AC és Skandináv fsz. -től északra lévő sekély ciklon közös áramlási rendszerében sarkvidékről érkező levegő jóvoltából.)
A hidegdepo közelsége adottá válik az év utolsó napjaira, ami képes átrendezni Európa időjárását, de ennek végkifejletét a jelek szerint január első hetében vagy annak első hétvégéjén élhetjük át mire futja majd abból.
Térképen 850-en gyönyörűen látszik az Európa térképének északi felén, hogy kezd az Északi Sarkvidéken beszakadni az AO index mínuszba, hiszen majdnem még nézni se kell, hogy nulla felé vagy lejjebb tendál. A NAO index dettó ebbe az irányba billeg, s nekünk nagyon fontos, hogy az is az legyen, ellenben Izlandi ciklongyárra lenne "hajtóanyag" a sarki hidegleszakadás.
Összegezve a olvasottakat: December utolsó napjaiban konkrét hidegfelhalmozódás, illetve kis "lefűződés" irányul Skandináv félszigettől nyugatra Izland és Brit Szk. irányába, de az aktuális mérsékelt övi európai áramlási viszonyok félblock és északi zónás jegyekben vannak. A kiéleződő hőmérsékleti kontraszt beindítja a gyorsabban lezajló áthelyeződési folyamatokat, s jelentősen megnőhet az esélye egy téli időjárási helyzetnek Nyugat- Közép- Európában.
Tartósságba nem bocsátkoznék, de ha figyelembe veszem az eddig "megszokott" Ac hajlamot térségünkben, kellően nagy adag hidegleszakadás esetén medi esélyektől a tartósan rajtunk maradó hetes száraz hidegen át minden féle szeráció lehet nyomás központok elhelyezkedésétől nagyban függően.
Most nem tartom valószínűnek, hogy gyorsan kipucolódna ez a leendő állapot. Egy laza 1 hetes téli (nappal is inkább mínusz mint plusz) és nem télies időre (mostani pár fokokra) teszem voksom.
Jók az előjelek.
Okosabbak a helyzetet illetőleg óév utolsó napján leszünk, talán addigra látni fogjuk mikor szándékozik északnyugat ,észak felől megjönni az a bizonyos hideg.
BOLDOG KARÁCSONYT MINDENKINEK!




Direkt linkek:
NAO:
Egy kicsit nehezen kezdem szavaim, szerintem idén nem is nagyon latolgattam a telet. "Nem volt mit, mi kiverje az ingerküszöbömet."
Mostanra a GFS kacérkodik "utolsó szalmaszálként" Karácsony utánra némi havacskával.
Jelenlegi GFS alapján Tisza vonalában érkezne észak felől.

A hosszútávú topik témájánál maradva a változékonyság jelei űridőben már tapasztalhatók. (Erről később lentebb.) A GFS rendületlenül adja üveggömb tartományban (még) 192 órán túl < x időpontokban. (Úgy fest jó lesz egy életre megjegyeznem, hogy a a gyenge La Nina egyúttal kedvezhet is a jobb télnek mint sem egy erősebb.)
A markánsabb változás európai jelei már 192 órán belülre értek, aminek hazánkra gyakorolt hatása napról napra nő és ennek folyományaként amatőr latolgatóként január első dekádjára de leginkább nagyjából jan 2 ás jan 10 közé klasszikus Brit Blockingot vagy annak egyéb blockoló Brit Izlandi Ac-t valószínűsítek, hozzánk pedig ényi áramlást.
(Azon belül már csak részlet kérdése, hogy ha itt landol a hideg hogy sikerül medi? hf? csapdék? halmazállapot? területi lefedettség? Ez 144 órán belüli történet, amibe jóslásba most nem bocsátkoznék.
Bővebben, adatokba kapaszkodva:
A mostani makrokép is nagyjából meridionális, attól függetlenül hogy nincs még hideg, illetve nincs a közelben elegendő, amit letud forgatni hozzánk. A csapadék is adott, csak a hideg hiányzik. Ami pedig ilyenkor lenni szokott, hogy ezt általában félzónás, zónás jegyek követik. Ha csak az ECM lapozom végig északi zónalitás-> félblock - > megint északi zóna. Ha a GFS -t nagyjából hasonló helyzet.
A régi metnetes öregektől 2010 előtti és alatti időben mindig azt tanultam, hogy az északi zóna egy fokkal jobb makroszinoptikai helyzet mint a sima zóna, mert előbbi esetén nem pucolódik ki a hidegbázis Európa közeléből, ami 5-6 napos távban blockba le is tud fűződni, ha akad egy Rossby hullám amit meglovagol avagy lefűződik nahh, akár a mi szélességünkre. Másik érv az északi zóna mellett, hogy viszonylag egyben tartja a hidegbázist Európára néző felén.
A változás pedig elég szembeötlően ott van szakavatott amatőr vagy hivatalos szemeknek, mivel mindkét nagy "királyi" modell / GFS, ECMWF / nagyjából egyetért, hogy 144 órától ( dec.29) Izland és attól északra elhelyezkedő vizek felett tartósan megveti magát a 850hPalon vett ~1550m () -10 - (-15) fok körüli légtömeg. (Az ottani stabil Grönlandi AC és Skandináv fsz. -től északra lévő sekély ciklon közös áramlási rendszerében sarkvidékről érkező levegő jóvoltából.)
A hidegdepo közelsége adottá válik az év utolsó napjaira, ami képes átrendezni Európa időjárását, de ennek végkifejletét a jelek szerint január első hetében vagy annak első hétvégéjén élhetjük át mire futja majd abból.
Térképen 850-en gyönyörűen látszik az Európa térképének északi felén, hogy kezd az Északi Sarkvidéken beszakadni az AO index mínuszba, hiszen majdnem még nézni se kell, hogy nulla felé vagy lejjebb tendál. A NAO index dettó ebbe az irányba billeg, s nekünk nagyon fontos, hogy az is az legyen, ellenben Izlandi ciklongyárra lenne "hajtóanyag" a sarki hidegleszakadás.
Összegezve a olvasottakat: December utolsó napjaiban konkrét hidegfelhalmozódás, illetve kis "lefűződés" irányul Skandináv félszigettől nyugatra Izland és Brit Szk. irányába, de az aktuális mérsékelt övi európai áramlási viszonyok félblock és északi zónás jegyekben vannak. A kiéleződő hőmérsékleti kontraszt beindítja a gyorsabban lezajló áthelyeződési folyamatokat, s jelentősen megnőhet az esélye egy téli időjárási helyzetnek Nyugat- Közép- Európában.
Tartósságba nem bocsátkoznék, de ha figyelembe veszem az eddig "megszokott" Ac hajlamot térségünkben, kellően nagy adag hidegleszakadás esetén medi esélyektől a tartósan rajtunk maradó hetes száraz hidegen át minden féle szeráció lehet nyomás központok elhelyezkedésétől nagyban függően.
Most nem tartom valószínűnek, hogy gyorsan kipucolódna ez a leendő állapot. Egy laza 1 hetes téli (nappal is inkább mínusz mint plusz) és nem télies időre (mostani pár fokokra) teszem voksom.
Jók az előjelek.
Okosabbak a helyzetet illetőleg óév utolsó napján leszünk, talán addigra látni fogjuk mikor szándékozik északnyugat ,észak felől megjönni az a bizonyos hideg.
BOLDOG KARÁCSONYT MINDENKINEK!
Direkt linkek:
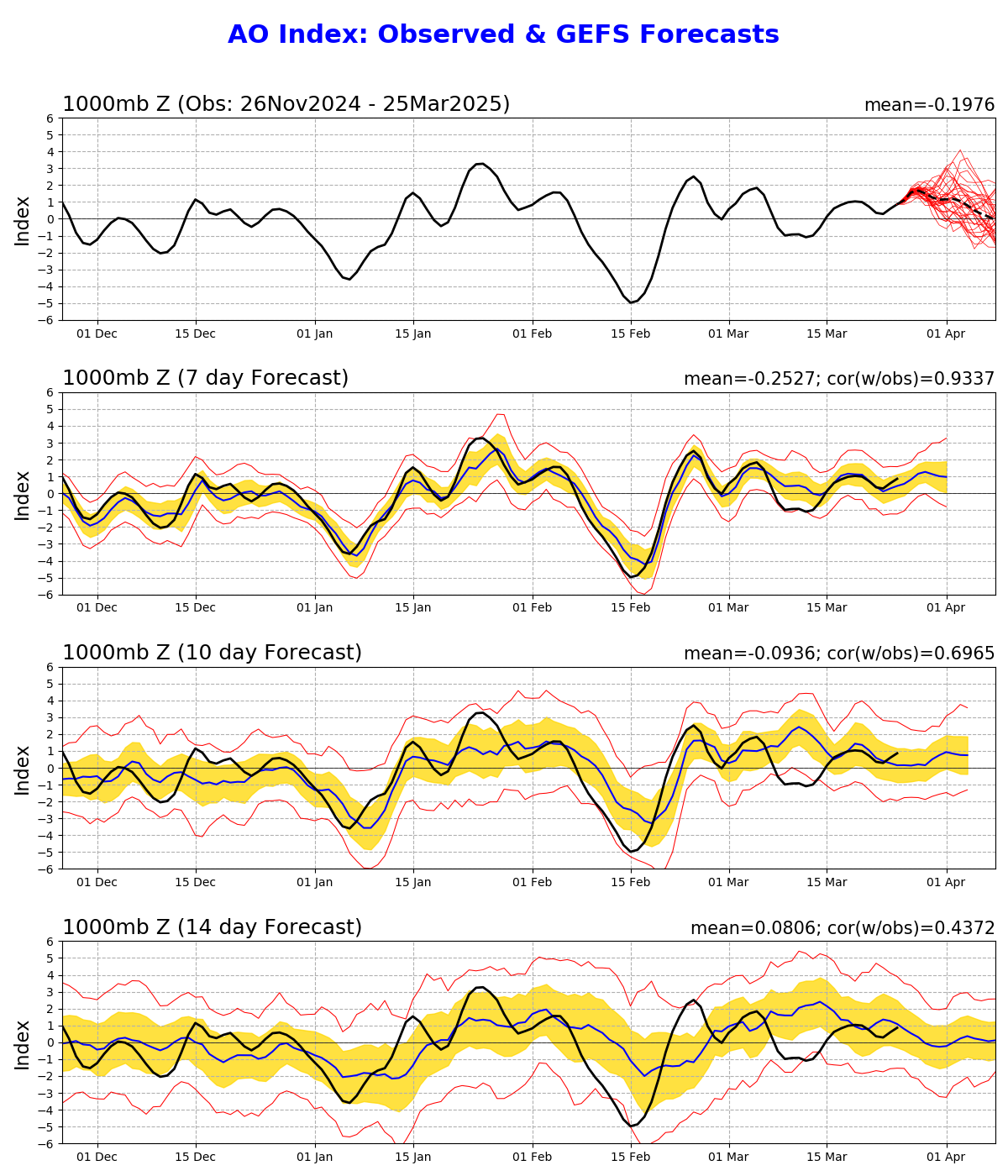
NAO:
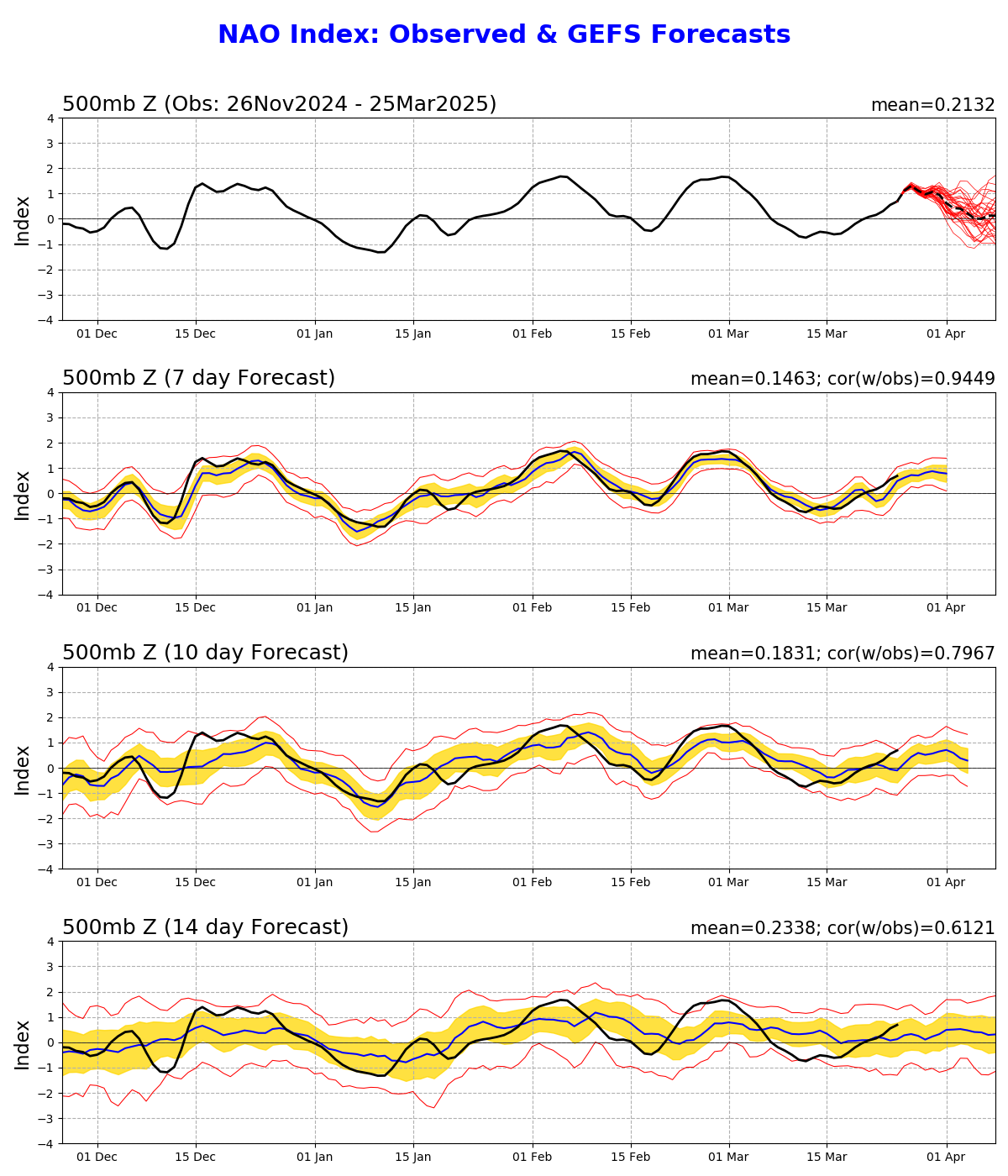
Kicsit gondolkodtam, hogy megéri-e írni a hosszabbtávról bármit, mert a poláris örvény fejlődését elég jól lehet látni, de a troposzférikus viszonyok nagyon nagy káoszt mutatnak, pláne az Euro-Atlanti térség.
10-e után már nemcsak stagnál, hanem gyengül is az örvény. Ez együtt jár az örvény Északnyugat-Ázsia (Novaja Zemlja térsége) fölé húzódásával, egy markánsabb Csendes-óceán feletti sztratoszférikus gerinc kialakulásával, vagyis megint vissza az egyhullámos helyzetbe. (Az örvény legutóbbi erősödése pont a kéthullámos szakaszra esett nov. 25-e óta, 2. ábrán alsó felén a -200 gpm alatti színezett wave-1 anomália).
Jellemző még a "vezér"teknő nyugat felé dőlése a magassággal. Ez Észak-Szibéria feletti alacsony geopotenciálok megjelenését jelenti. Ez elég nyugatra lehet ahhoz, hogy Uráli anticiklon se nagyon alakuljon ki, viszont legalább havazgathat gyakran Szibéria egyes térségeiben. Egyébként az Eurázsiai hóborítottság most átlag alatti, talán ez inkább felfelé korrigálhat.
Változás talán csak a hónap utolsó dekádjában, de inkább csak karácsony után lehet, akkor ez a helyzet gyengülhet, és AC-k is jobban megtelepedhetnek az orosz területek északabbi részein is. Legalábbis a többhetes ezt pedzegeti. Abban az időszakban meg is áll az ECM többhetes átlaga szerint az örvény gyengülés.
Ami a mutatott erősebb sztratoszférikus melegedési hullám lehetőségét illeti: szerintem az örvény gyengülés a sztratoszféra belső állapotából fakad a folyamat végén egyre inkább. Nem érzem stabilnak, konzisztensnek futásról futásra a felfelé áramló fluxosokat. Illetve az Euro-Atlanti szektorban nagy a káosz, onnan nem biztos, hogy kaphat bármilyen triggert a sztratoszféra örvénye. (12-es futás, ahol a 100 K*m/s feletti fekete kontúrok az ábrán lent szinte teljesen hiányoznak).
Ha mégis lenne nagyobb gyengítő fluxus akkor lehetne erősebb örvénygyengülés, valódi minor warming szerű helyzettel. Ha ez mégis bekövetkezik, az jelentősebben is változtathat a kilátásokon.
De az Atlanti-térségben inkább a ciklonaktivitás növekedése is felfedezhető a hónap derekától (emelkedő NAO index, 1. klaszter). Mintha arra is lenne próbálkozás, hogy a gyengülés során a valószínűbbnek látszó forgatókönyv szerint fennmaradó legalább átlagos erejű örvény, fenti pozitív AO mégis "leszivárog" végül a troposzférába.
Kérdés, hogy karácsonytól és az év végén mi történik, megtelepszik-e a pozitív NAO/AO fázis, és inkább csak tőlünk keletebbre lesznek magasabb szélességeken AC-k. Persze hosszabb távon ez utóbbi nem lenne annyira rossz, ha jönne rá megfelelő makrokép a későbbi hetekben.
10-e után már nemcsak stagnál, hanem gyengül is az örvény. Ez együtt jár az örvény Északnyugat-Ázsia (Novaja Zemlja térsége) fölé húzódásával, egy markánsabb Csendes-óceán feletti sztratoszférikus gerinc kialakulásával, vagyis megint vissza az egyhullámos helyzetbe. (Az örvény legutóbbi erősödése pont a kéthullámos szakaszra esett nov. 25-e óta, 2. ábrán alsó felén a -200 gpm alatti színezett wave-1 anomália).


Jellemző még a "vezér"teknő nyugat felé dőlése a magassággal. Ez Észak-Szibéria feletti alacsony geopotenciálok megjelenését jelenti. Ez elég nyugatra lehet ahhoz, hogy Uráli anticiklon se nagyon alakuljon ki, viszont legalább havazgathat gyakran Szibéria egyes térségeiben. Egyébként az Eurázsiai hóborítottság most átlag alatti, talán ez inkább felfelé korrigálhat.



Változás talán csak a hónap utolsó dekádjában, de inkább csak karácsony után lehet, akkor ez a helyzet gyengülhet, és AC-k is jobban megtelepedhetnek az orosz területek északabbi részein is. Legalábbis a többhetes ezt pedzegeti. Abban az időszakban meg is áll az ECM többhetes átlaga szerint az örvény gyengülés.

Ami a mutatott erősebb sztratoszférikus melegedési hullám lehetőségét illeti: szerintem az örvény gyengülés a sztratoszféra belső állapotából fakad a folyamat végén egyre inkább. Nem érzem stabilnak, konzisztensnek futásról futásra a felfelé áramló fluxosokat. Illetve az Euro-Atlanti szektorban nagy a káosz, onnan nem biztos, hogy kaphat bármilyen triggert a sztratoszféra örvénye. (12-es futás, ahol a 100 K*m/s feletti fekete kontúrok az ábrán lent szinte teljesen hiányoznak).

Ha mégis lenne nagyobb gyengítő fluxus akkor lehetne erősebb örvénygyengülés, valódi minor warming szerű helyzettel. Ha ez mégis bekövetkezik, az jelentősebben is változtathat a kilátásokon.
De az Atlanti-térségben inkább a ciklonaktivitás növekedése is felfedezhető a hónap derekától (emelkedő NAO index, 1. klaszter). Mintha arra is lenne próbálkozás, hogy a gyengülés során a valószínűbbnek látszó forgatókönyv szerint fennmaradó legalább átlagos erejű örvény, fenti pozitív AO mégis "leszivárog" végül a troposzférába.


Kérdés, hogy karácsonytól és az év végén mi történik, megtelepszik-e a pozitív NAO/AO fázis, és inkább csak tőlünk keletebbre lesznek magasabb szélességeken AC-k. Persze hosszabb távon ez utóbbi nem lenne annyira rossz, ha jönne rá megfelelő makrokép a későbbi hetekben.
Komoly, télbe forduló átrendeződés december első 4-5 napjáig véleményem szerint nem várható Európa nagy részén. Sajnos jelenleg kiszorult a hideg nagy része Szibériából, de ez ilyen tájt nem ritka. 72 óra múlva ugyanakkor egy ciklon fog tevékenykedni a sarkkörnél, egészen pontosan a Spitzbergák és Norvég partok közötti, tenger feletti középponttal.
Link
Link
Ez a ciklon egy jó ideig örvénylik majd a sarkvidék felett és a nyugat-európai bivaly előoldalt okozó ciklon szépen, lassan beleolvadhat, majd egy kiterjedt ciklonrendszert alakíthatnak. E mögött épülhet ki egy AC híd Izland térsége és az Atlanti-óceán keleti területe felett.
Link
Itt már teljesen jól látható, hogy a hidegmag szépen elkezdi összeszedni magát Szibéria és a sarkvidék felett, köszönhetően annak a markáns ciklonrendszernek, mely várhatóan fel is őrlődik majd.
Link
Távoli ugyan, de 240 óránál már csak sekély ciklonként funkcionálna és egyre hidegebb levegő töltené ki Szibériát.
A korábbi AC híd az Oroszok felett megerősödve, jó fagyos légtömeggel kitöltve tovább segítené elő egy komolyabb hidegbázis kiépülését. Jelenlegi ECMWF-en kissé erős lenne az óceáni viharciklon és túl keletre robbana be, ezért a korábbi Skani AC próbálkozás nem tudna összehozni egy esetleges téltámadást, de ez még egyébként nincs lefutva.
A mondandóm lényege igazság szerint az, hogy nagyjából December 5-10 között mutatkozhat számottevő esélye akár egy jelentős makrováltásnak, amikor is tőlünk északkeletre már tetemes mennyiségű hideg halmozódhat fel, illetve beleértve ebbe Szibériát is. Ősz óta hatalmas az AC uralom a kontinensen, láthattuk hogy sarkvidék lehűlése ellenére alig-alig volt viharciklon is az óceánon, de egyáltalán ciklon is. Most átmenetileg kissé megszaporodnak majd, de jelen cirkuláció folytatódásával nagyon valószínű, hogy gyorsan visszatérnek majd a blockingos helyzetek is.
Link
Link
300 óra magasságában látható, hogy szépen kiépül és vaskosodik az újabb hidegdepó Eurázsiában. Szépen komótosan, de egyre nagyobb teret hódíthat majd a hideg, ez látható is a modelleken jelenleg. Meggyőződésem, hogy fokozatosan, de a tél egyre erősebben fog próbálkozni a jövő hónap folyamán a visszatérő blockingos helyzetekkel! Zonalitásra most is csekély az esély és ha valóban az őszi verkli folytatódik a tél első 2 hónapjában, akkor bizony nem lesz enyhe telünk. Ehhez nem ártana egy jelentősebb SSW is, akár egy Polar Splitbe torkollva és örvény széteséshez vezetve, csak hogy hab is legyen a tortán. A jelenlegi helyzetkép alapján szépen elkezd gyengülni ismét az örvény és 10hPa-n a szél sebessége szépen lelassulhat januárhoz közeledve...
Link
Link
Ez a ciklon egy jó ideig örvénylik majd a sarkvidék felett és a nyugat-európai bivaly előoldalt okozó ciklon szépen, lassan beleolvadhat, majd egy kiterjedt ciklonrendszert alakíthatnak. E mögött épülhet ki egy AC híd Izland térsége és az Atlanti-óceán keleti területe felett.
Link
Itt már teljesen jól látható, hogy a hidegmag szépen elkezdi összeszedni magát Szibéria és a sarkvidék felett, köszönhetően annak a markáns ciklonrendszernek, mely várhatóan fel is őrlődik majd.
Link
Távoli ugyan, de 240 óránál már csak sekély ciklonként funkcionálna és egyre hidegebb levegő töltené ki Szibériát.
A korábbi AC híd az Oroszok felett megerősödve, jó fagyos légtömeggel kitöltve tovább segítené elő egy komolyabb hidegbázis kiépülését. Jelenlegi ECMWF-en kissé erős lenne az óceáni viharciklon és túl keletre robbana be, ezért a korábbi Skani AC próbálkozás nem tudna összehozni egy esetleges téltámadást, de ez még egyébként nincs lefutva.
A mondandóm lényege igazság szerint az, hogy nagyjából December 5-10 között mutatkozhat számottevő esélye akár egy jelentős makrováltásnak, amikor is tőlünk északkeletre már tetemes mennyiségű hideg halmozódhat fel, illetve beleértve ebbe Szibériát is. Ősz óta hatalmas az AC uralom a kontinensen, láthattuk hogy sarkvidék lehűlése ellenére alig-alig volt viharciklon is az óceánon, de egyáltalán ciklon is. Most átmenetileg kissé megszaporodnak majd, de jelen cirkuláció folytatódásával nagyon valószínű, hogy gyorsan visszatérnek majd a blockingos helyzetek is.
Link
Link
300 óra magasságában látható, hogy szépen kiépül és vaskosodik az újabb hidegdepó Eurázsiában. Szépen komótosan, de egyre nagyobb teret hódíthat majd a hideg, ez látható is a modelleken jelenleg. Meggyőződésem, hogy fokozatosan, de a tél egyre erősebben fog próbálkozni a jövő hónap folyamán a visszatérő blockingos helyzetekkel! Zonalitásra most is csekély az esély és ha valóban az őszi verkli folytatódik a tél első 2 hónapjában, akkor bizony nem lesz enyhe telünk. Ehhez nem ártana egy jelentősebb SSW is, akár egy Polar Splitbe torkollva és örvény széteséshez vezetve, csak hogy hab is legyen a tortán. A jelenlegi helyzetkép alapján szépen elkezd gyengülni ismét az örvény és 10hPa-n a szél sebessége szépen lelassulhat januárhoz közeledve...